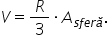Sfera (descriere, formule)
Tag-uri
Partajeaza in Google Classroom
Transcript
să vedem Care sunt formulele pentru
determinarea ariei și volumul unei
sfere mai întâi să vedem ce este
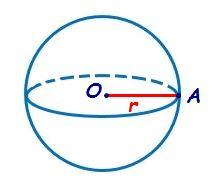
aceea o sferă și avem aici definiția
Mulțimea punctelor din spațiu situate
la aceeași distanță față de un
punct fix formează un corp în spațiu
numit sferă cu alte cuvinte dacă
ne alegem un punct fix de exemplu
acesta punctul fix se numește centrul
sferei atunci toate punctele din
spațiu Care sunt situate la aceeași
distanță față de acest punct fix
alcătuiesc un corp geometric numit
sferă și am reprezentat aici o
sferă putem să ne imaginăm foarte
ușor o minge de ping pong de exemplu
orice puncte am alege pe suprafața
acele mingi vor fi egal depărtate
de centrul ei pentru că are forma
unei sfere și putem să notăm centrul
sferei cu o chiar putem să trecem
și raza sferei Iată o notăm cu
R mare și avem aici sfera de centru
o și rază r mare Care sunt formulele
pentru determinarea ariei pentru
că aici nu putem să vorbim de o
arie laterală De ce avem aria sferei
este egală cu avem următoarea formulă
4 pi R pătrate volumul sferei este
egal cu avem patru pere la a treia
supra 3 nu vom demonstra nici una
din aceste două formule însă vom
face următoarea observație și anume
volumul sferei vrem să îl scriem
în funcție de aria sferei și e
foarte ușor de făcut acest lucru
volumul poate fi scris astfel 4
Pierre la a doua 4 tir pătrat și
ca să ajungem la această formulă
mai avem nevoie de aer supra 3
Păi De fapt am obținut avem aici
aria sferei înmulțită cu r supra
3 și astfel am obținut legătura
dintre volumul sferei Iată aici
și aria sferei să reținem aceste
două formule pentru determinarea
ariei și volumului unei sfere și
ușor de văzut faptul că nu avem
nevoie de niciun înălțime sau generatoare
pentru că sfera e determinată doar
de rasă și de centru Deci aria
sferei este patru pere pătrat volumul
este patru pere la 3-a supra 3
Sfera- definiție, formulele pentru arie și volumAscunde teorie X
Navigare în lectii
Cumpara abonament
