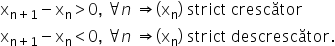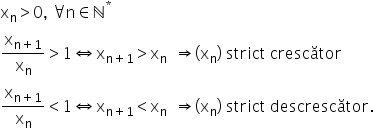Șiruri monotone (aplicații)
Tag-uri
Partajeaza in Google Classroom

Transcript
Haideți acum să facem un exercițiu
în care studiem monotonia unor
șiruri vă reamintesc că pentru
a studia monotonia unui șir Avem
două posibilități fie calculăm
Diferența a doi termeni consecutivi
comparăm cu 0 și calculăm raportul
la doi termeni consecutivi și îl
comparăm cu unu această a doua
modalitate se poate aplica numai
atunci când șirul are toți termenii
pozitivi Și începem cu punctul
A Avem un șir xn unde termenul
general este dat de Formula x n
egal cu n supra 3n plus 2 Haideți
să calculăm Diferența a doi termeni
consecutivi x 1 minus x n ca să
aflăm pe x n plus 1 în formula
termenului general o să înlocuim
pe n cu n plus 1 și obținem n plus
1 supra 3 pe lângă n plus 1 plus
2 minus n supra 3n plus 2 egal
n plus 1 supra 3n plus 5 minus
n supra 3n plus 2 aducem la numitor
comun amplificăm prima fracție
cu 3n plus 2 și a doua fracție
cu 3 ani plus cinci și obținem
în plus 1 pe lângă 3 n plus 2 minus
n pe lângă 3 n plus 5 totul supra
3n plus 5 pe lângă 3 n plus 2 egal
desfacem parantezele Avem 3 m pătrat
plus doi n plus 3 n este 5n plus
2 minus 3 n pătrat minus 5 n totul
supra 3n plus 5 pe lângă 3 n plus
2 egal se reduce 3n pătrat la fel
și 5n și obținem 2 supra 3n plus
5 pe lângă 3 n plus 2 Nu este cazul
să desfacem parantezele și la numitor
pe noi ne interesează doar semnul
acestei expresii din moment ce
e n este număr natural nenul această
fracție va fi pozitivă Așadar șirul
x n este un șir strict crescător
continuăm cu punctul b la punctul
B avem șirul x n unde termenul
general este dat de Formula an
plus 5 supra m pătrat plus 1 Haide
să calculăm și de data aceasta
diferența x n plus 1 minus x n
egal Înlocuim pe r cu r plus 1
și obținem n plus 1 plus 5 supra
n plus 1 totul la pătrat plus 1
minus m plus 5 supra m pătrat plus
1 egal în plus 6 supra n pătrat
plus doi n plus unu plus unu adică
plus 2 minus n plus 5 supra n pătrat
plus 1 egal aducem la numitor comun
amplificăm cu n pătrat plus 1 și
aici amplificăm cu n pătrat plus
doi n plus 2 egal un plus 6 pe
lângă n pătrat plus 1 minus m plus
5 pe lângă n pătrat plus doi n
plus 2 totul supra m pătrat plus
doi n plus 2 pe lângă n pătrat
plus 1 egal voi continua mai jos
desfacem parantezele avem n la
puterea a treia plus n plus 6 n
pătrat plus 6 minus aici avem minus
în fața acestor paranteze Deci
toți termenii vor avea semnul minus
idila a treia minus 2 n pătrat
minus 2 n minus 5 n pătrat minus
10 n minus 10 totul supra m pătrat
plus 2 n plus 2 pe lângă n pătrat
plus 1 egal se reduce aer la a
treia cu minus n la a treia apoi
6n la a doua minus 2x la a doua
este 4 n la a doua minus 5 L la
a doua este minus n la pătrat minus
2 n este minus n minus 10 n minus
11 n 6 minus 10 minus 4 totul supra
n pătrat plus doi n plus doi pe
lângă m pătrat plus 1 egal putem
să scrie pe minus în fața liniei
de fracție și avem n la a doua
plus 11 n plus 4 supra n la a doua
plus doi n plus doi pe lângă n
la a doua plus 1 această fracție
este pozitivă și cu minus surzi
față la fi negativă oricare ar
fi n număr natural nenul Așadar
șirul nostru x n este strict descrescător
întrucât Diferența a doi termeni
consecutivi este întotdeauna negativă
pentru orice număr natural nenul
continuăm cu punctul c avem șirul
x n egal cu n supra 3 la puterea
n Haide de data aceasta să calculăm
raportul la doi termeni consecutivi
se poate observa că acest șir are
toți termenii pozitivi n este număr
natural de 3 la puterea n va fi
număr natural prin urmare toată
această fracție va fi număr pozitiv
Marcu lemn Așadar raportul x n
plus 1 supra x n egal ca să nu
lucrăm cu fracție supraetajată
o să îl scriu mai întâi pe x n
plus 1 n plus 1 supra 3 la puterea
n plus 1 ori investesc cea de a
doua fracție 3 la n supra n egal
3 la n plus 1 se simplifică cu
3 la n și de rămâne un trei obținem
n plus 1 supra 3n Aceasta este
o fracție subunitară pentru că
m plus 1 este mai mic decât 3n
putem chiar să verificăm acest
lucru n plus 1 este mai mic decât
3n trecem toți termenii intru în
membru obținem 2n minus unu mai
mare strict decât 0 oricare ar
fi n număr natural nenul Aceasta
este o relație adevărată Iată pentru
n egal cu 1 Avem doi minus unu
unu Deci mai mare decât 0 Așadar
raportul dintre doi termeni consecutivi
este mai mic decât 1 prin urmare
șirul x n este un șir strict descrescător
în general această metodă de a
studia monotonia unui șir este
practică atunci când an apare la
exponent ca să putem face aceste
simplificări continuăm cu punctul
de șirul xn are formula termenului
general suma k de la 1:00 și până
la n din 1 supra 4 la puterea k
plus 1 calculăm diferența x n plus
1 minus x n Dacă x este o sumă
de n termeni atunci x n plus unu
va fi o sumă de n plus 1 termeni
Așadar formula termenului de rang
n plus 1 va fi suma k de la 1 până
la n plus 1 din 1 supra 4 la k
plus 1 minus Sumac apa de la 1
și până la n din 1 supra 4 la k
plus 1 egal această sumă de n plus
1 termeni se mai poate scrie și
astfel sumă k egal 1 până la n
din 1 supra 4 la k plus unu Deci
până aici avem suma primilor n
termeni la care se mai adaugă ultimul
termen Iar acest ultim termen se
obține înlocuind pe k cu n plus
unu și avem 1 supra 4 la n plus
unu plus unu Deci până aici Am
scris prima sumă aceasta și urmează
minus suma k de la 1 și până la
n din 1 supra 4 la k plus 1 egal
aceste două sume se reduc și ne
mai rămâne termenul 1 supra 4 la
puterea n plus unu plus unu care
se mai poate scrie 1 supra 4 ori
4 la n plus 1 in c n este număr
natural nenul această fracție este
întotdeauna pozitivă oricare ar
fi n număr natural nenul Așadar
șirul x n este strict crescător


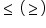 atunci șirul este crescător (descrescător).
atunci șirul este crescător (descrescător).