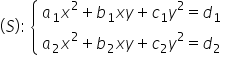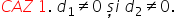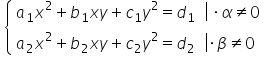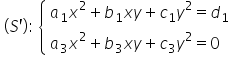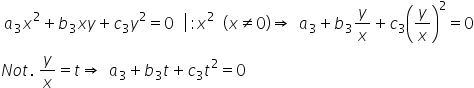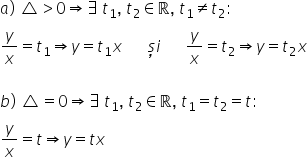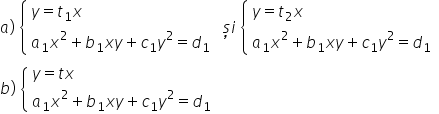Sisteme de ecuații omogene

în această lecție ne vom opri asupra

sistemelor de ecuații omogene aceasta

se constituie ca o continuare naturala

lecțiilor 3 sedinte lecții în care

am supus atenției voastre ecuația

de gradul al doilea și sisteme

constituite cu ecuații de gradul

al doilea întrucât sistemele omogene

se mai definesc și ca sisteme ale

căror rezultate sau coloană rezultat

cum îi spune sau coloana termenilor

si nu este 0 în întregime un astfel

de sistem este de forma notat este

mine a 1 x pătrat plus pe 1 x y

plus si 1 Y8 egal cu d 1 respectiva

ecuație pe de tot de gradul al

doilea a 2 x pătrat plus b 2 x

y plus 2y pătrat egal cu d2 sistemul

esti vă spuneam la am notat cu

a 6 sistem se numește omogeni deoarece

atât primul cât și cel de al doilea

polinom al sistemului conțin doar

monoame de același grad un polinom

mă refer la partea stângă Dacă

vorbesc de egalitate vorbesc practic

de ecuația și acum vă spuneam da

în cazul meu ecuații de gradul

al doilea manele a unui pătrat

și a 2x pătrat au același grad

2 la fel și Mona mele b 1 x respectiv

b 2x y Da gradul întâi are X1 gradul

1 are cu astfel că prin înmulțire

ele vor duce la același grad 2

Da și ce unui pătrat respectiv

C2 pătrat au În egală măsură gradul

al doilea presupunem pentru că

termenii de pere a ecuațiilor sistemului

sunt diferiți de zero adică d1

și d2 Aceștia sunt termenii Deva

în aceste condiții există numerele

reale Alfa și Beta diferite de

0 astfel încât a Alfa la de 1 plus

2 egal cu 0 De exemplu dacă Alfa

egal cu 1 evidențieri diferit de

0 b ar fi minus 1 supra 2 care

nu OTV ident este diferit de zero

În condițiile în care așa cum vă

spuneam a presupus că de 1 respectiv

de doi sunt diferite de 0 algoritmul

de rezolvare acest algoritmi este

practic o dispunere pe pași Da

a modalității de rezolvare a sistemelor

de ecuații omogene sisteme pe care

în această lecție vila supun atenției

se înmulțește prima ecuația sistemului

cu alfa De ce ca să obțină Alpha

D1 se înmulțește a doua ecuația

sistemului cu peta De ce ca să

obțin peta Z2 încă o dată vară

prima ecuația sistemului are termen

liber când îl înmulțesc cu Alpha

voi obține Alpha de 1 a doua ecuația

sistemului are termen liberte 2

când îl înmulțesc cu Veta voi obține

pe tate doi și atunci inevitabil

etapa următoare sau pasul următor

de de urmat este că ecuațiile echivalente

obținute să se adune ca să obținem

această relație de care Comentați

ecuația obținută la pasul trecut

devine a doua ecuația sistemului

prima ecuația sistemului fiindcă

fie obține astfel un sistem echivalent

cu sistemul inițial tot sistemul

notat de noi este astfel așa cum

vă spuneam se înmulțește cu alfa

se înmulțește cu Beta Alfa înmulțit

cu această ecuație se înmulțește

cu toți termenii ecuații Da Mona

mele conținute în ecuație și atunci

Alfa a 1 x pătrat plus Alfa b 1

x y plus al face unui pătrat egal

așa cum spuneam Alfa de 1 pe același

principiu și pe Da după cum spuneam

acestea trebuiesc adunate în acest

caz prima ecuații așa cum am spus

se copiază Da a unui pătrat b 1

x y plus si 1 Y8 egal cu de 1 și

a tatuați spuneam devine ecuația

echivalentă obținută prin adunarea

celor Două ecuații astfel corect

centrului pătrat va fi Alfa a umple

speta A2 coeficientului xy va fi

alfabeta pe 2 respectiv coeficientului

y pătrat va fi el face 1 plus speta

C2 pentru cât mai buna vizualizare

și înțelegere algoritmului voi

nota în continuare coeficienții

Comentați cu a 3 b 3 respectiv

C3 astfel Sistemul nostru devine

sistemul echipolent notat de mine

cu exprimi și anume a unui pătrat

de 1xy ce unui pătrat Da egal cu

d 1 respectiv după notație a 3x

pătrat b 3 x y spectiv si 3 y o

tot ce mă avantajează în toată

povestea asta este că la acest

moment am obținut rezultatul ecuații

2 în sistemul lui 0 și aceasta

îmi permiteți să trec la următoarea

etapă a rezolvări sistemul astfel

că în condițiile în care am crescut

la început că D1 este diferit de

0 x egal cu 0 respectiv egal cu

0 nu poate să fie soluția systema

astfel putem presupune în continuare

că x este diferit de 0 în aceste

condiții pot trece la împărțirea

ecuații 2 cea la care am obținut

rezultatul 0 așa cum iau și propus

da prin x pătrat astfel obțin A3

coeficientul Da x pătrat supra

x pătrat plus b trecutul lui x

y și atunci x y supra x pătrat

respectiv C3 y pătrat supra x pătrat

egal cu 0 supra x pătrat ecuația

nou ținută este A3 plus pe 3y pe

x si y x totul la pătratul servat

gradele Da sunt doi în ambele cazuri

drept pentru care pot să scriu

ca fracție totul la a doua în aceste

condiții vom nota supra x egal

cu tete fiind o valoare reală și

ecuația mea să devină si 3 pe pătrat

Da plus 3 plus 3 egal cu 0 Aceasta

este o ecuație de gradul al doilea

cu coi 15 ani ecuații ce poate

fi rezolvată fără discuții după

rezolvare ecuații se pot obține

trei categorii de rădăcini după

cum bine cunoaște și anume a pot

să am rădăcini reale și distincte

Deci te unul diferite te 2 Real

pot să am rădăcinile reale și că

are Adică T1 egal cu 2 respectiv

rădăcini complexe Evident nu sunt

reale atunci când vorbim de situațiile

a și b și toții în care T1 și T2

sunt reale Revenim la notația făcută

notația de aici Da Și n care expira

egal cu t în cazul ce când nu am

toate cinci reale sistemul nu admitere

soluții reale și atunci nu va face

subiectul lecției în cauză atunci

când ecuația așa cum spuneam are

rădăcini reale se deplasa si tu

ție după casă în cazul amic yt-14501

x și y x egal cu T2 caz în care

a fi t2x în cazul b vorbeam de

rădăcini egal y pe x egal cu 1

sau pe 2 tot aia e înțelegând din

asta că e grav ati venit pe unul

în ambele situații în care așa

cum spuneam de cine sunt reale

Da se continuă rezolvarea sistemului

esti stemulin inițial cu pentru

situația S1 ep egal cu t1x la 12:00

situația asta da Și a doua ecuații

a sistemului de fapt prima și foarte

important a doua situație dacă

îmi dai pe x arate doi de y egal

cu 2x și așa cum spuneam prima

ecuația sistemului de vin în acest

moment a doua ecuația sistemului

a unui pătrat plus pe unui surplus

c unui pătrat egal cu d pe situația

b este egal cu Teo nu e și prima

ecuație a sistemului astfel după

ce am revenit la substituției și

am obținut aceste sisteme S1 S2

Da înțeleg că găsesc sisteme ce

conțin o ecuație de gradul întâi

și una de gradul al 2 astfel de

sisteme se pot rezolva În condițiile

în care în lecția precedentă au

fost discutate la începutul acestei

lecții și mai clar înaintea de

algoritmi de rezolvare am presupus

că d1 și d2 sunt nenul vă arătam

eu sau vă exprimam către unul diferite

de zero respectiv de 2 diferit

de 0 specificat că în situația

în care de unul sau de doi sunt

Moni sistemul sistemul inițial

va avea formă spre în acest caz

algoritmul de rezolvare expuse

în lecție de la momentul în care

stau ținut formă echivalentă a

sistemului este pentru o mai bună

înțelegere a algoritmului de rezolvare

propun în continuare câteva exemple

și mai clar două exemple exemplu

să se rezolve sistemul de ecuații

x pătrat plus 3y plus pătrat egal

cu minus 2 respectiv x y plus pătrat

egal cu 4 Deci așa cum vedeți ambele

ecuații sunt de gradul al doilea

În egală măsură îți trebuie să

Observați în această situație că

D1 Teoretic este minus 2 D2 Teoretic

este 4 ambele variabile fiind diferite

de 0 pentru Rezolvarea acestui

sistem este necesar să parcurgem

pașii aferenți algoritmului mai

sus prezentate cum spuneam valoarea

de unui teoretică este minus 2

valoarea de 2 teoretică este 4

în acest caz se înmulțește ecuația

1 a sistemului cu 2 și se adună

la cea de a doua ecuații astfel

ecuația 1 a sistemului de vine

2 x pătrat plus 6x y plus 2x pătrat

egal cu minus 4 spuneam Cele Două

ecuații se vor aduna obținând iusti

astăzi 2x pătrat ar fi plus 0 1

m x pătrat aici Da plus 7 x y plus

3 y pătrat egal cu 0 ecuația 1

obținută anterior se rezolvă după

cum urmează vă aduceți aminte trebuia

să împărțim la x pătrat astfel

ecuația 2x pătrat plus 7 x y plus

3 pătrat egal cu zero da devine

2 x pătrat supra x pătrat plus

7 supra x pătrat plus 3 egal cu

pătrat supra x pătrat astfel 3

y supra x totul la pătrat plus

7 y supra x plus 2 egal cu 0 pentru

rezolvarea ecuației obținute este

indicat să notăm ac egal cute t

fiind o valoare real astfel obținem

ecuația 3x pătrat plus 7 t plus

2 egal cu 0 cântă de pătrat minus

patru ace Da calculat 25 este pozitiv

prin urmare pe un schit a 2 x diferit

folosind formula minus b plus minus

radical din Delta supra 2-a prin

simpla înlocuire obținem câte unu

egal cu minus 2 respectiv T2 egal

cu minus 1 supra 3 așa cum spuneam

confort teorii După obținerea valorilor

reale T1 și T2 este obligatoriu

să Vap la notația făcută astfel

notația făcută erai pe x egal cute

astfel așa cum spuneai pe a fiecărui

Deci prima soluție obțin respectiv

x egal cu minus 1 pe 3 spuneam

cea de a doua ecuația sistemului

devine practic ecuația coacerea

sistemului în cazul meu Ecuația

a doua și anume x y plus y pătrat

egal cu 4 respectiv în a doua situație

x y x egal cu pas astfel egal cu

minus 2x x y plus y pătrat egal

cu 4 x da în loc de x minus 2 plus

în loc de x y y minus 2x de data

aceasta la pătrat egal cu 4 și

anume minus 2x pătrat orice la

puterea a doua are Semnul plus

indiferent de semn Deci patru pătrate

egale cu 4 înțelegând 2 pătrat

egal cu 4 ceea ce pret ulei și

poate duce la obținerea soluții

x egal cu plus minus radical din

2 prin simpla înlocuire se determină

și y la acest moment obținând doar

x astfel că va fi minus 2 plus

minus radical din 2 la prima soluția

sistemului este egal cu minus 2

radical din 2 Pentru x egal cu

radical din 2 egal cu 2 radical

din 2 cel de al doilea sistem sistemul

notate de mine cu b la a doua plus

pătrat egal cu patru așa cum spuneam

prin substituție Deci înlocuirea

efectivă a lui x3y ajunge la relația

x y y egal cu soluțiile în acest

caz nu sunt reale pentru că în

aer da nu poți să obții o valoare

negativă pentru ceva ridicat la

pătrat temul în cazul nostru va

avea doar soluțiile x egal cu radical

din 2 cu AC egal cu minus 2 radical

din 1 și x egal cu minus y egal

cu 2 radical din 2 soluții reale

ale sistemului în continuare un

al doilea exemplu pe care Vic Crăciun

atenție este 2 3 x y x y pătrat

egal cu 0 respectiv x y plus pătrat

egal cu în acest caz d1 și d2 sunt

nori acest fapt face ca sistemul

să fie mai ușor de rezolvat și

nu mai este cazul sau nu mai necesar

să înmulțim ecuații cu constante

nenule astfel încât după aceea

să adunăm și să obținem acei termenii

pe Nuți astăzi în cazul nostru

putem trece direct la algoritmul

de rezolvare de la etapa în care

termenul liber ar fi fost obținut

0 împărțim așa cum bine știți Phoenix

pătrați obținem 2 pătrați pe ax

pătrat 3 x y supra x pătrat egal

pătrat supra x pătrat egal cu 0

Da după simplificare se obține

2 plus 3 pe lângă x y x plus y

x totul la obținem ecuația te pătrat

plus 3 plus 2 egal cu 0 ecuație

Ce este rezolvată Delta obținut

este pozitiv iar înțeleg t1 t2

reale diferite astăzi pe unul va

fi misto E respectiv pe 2 minus

1 așa cum am reținut Revenim la

notație cazul unul va fi cel în

care suflă x egal cu minus 2 cazul

lui va fi acela în care cifra x

va fi egal cu minus unu cea de

a doua ecuația sistemului x x plus

y pătrat egal cu 0 the divine și

este în continuare a doua ecuația

sistemului în aceeași ordine de

idei sistemul amic sistemul panic

Da sisteme ce urmează a fi calculate

separat Ospen Sistemul a este sistemul

minus 2x mai mic wați x y plus

pătrat egal cu 0 substituția făcută

și anume loc de x minus 2 plus

2 totul la pătrat egal cu 0 obținem

astfel 2 pătrat egal cu zero moment

în care fără discuții pixuri ar

trebui să fie 0 Da atunci când

x este 0 nu se poate accepta ca

soluție deoarece fracția yx-1000a

calcul 0 obținut din calcul nu

este acceptat sau nu poate fi soluție

a sistemul sistemul sistemul în

care se respectă x y plus de pătrat

egal cu 0 prin acea metodă de substituție

Deci prin înlocuirea lui y egal

cu minus X în cea de a doua ecuație

conduce la o relație adevărată

între o infinitate de cazuri sau

o așa numită identitatea adevărată

moment în care Da 0 egal cu 0 identitatea

adevărată a trage de la sine că

sistemul admite o infinitate de

soluții reale de forma x egal cu

k iar y egal cu minus k Deci soluții

fiica sistem nu va fi egal cu cai

cred că egal cu minus ca unde k

este o valoare reală