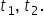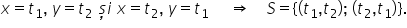Sisteme de ecuații simetrice
Tag-uri
Partajeaza in Google Classroom

Transcript
vom vorbi în această Lecție despre
a sisteme simetrice mai întâi Haideți
să vedem Ce înțelegem prin intru
ecuație simetrică Să privim puțin
aceste Două ecuații cu două necunoscute
Iată prima ecuație 2x plus 7 x
y plus 2y egal cu 10 Haideți să
înlocuim necunoscuta x cu y și
pe y înlocuind necunoscuta x cu
y obținem aceeași ecuație acestea
sunt două exemple de ecuații simetrice
însă următoarea ecuație 3 plus
x minus y egal cu 0 nu este ecuația
simetrică deoarece în acest caz
necunoscutele x și y au semne contrare
având în vedere că o ecuație simetrică
nu se schimbă când Înlocuim pe
x cu y rezultă cu 8 c soluție de
forma x 0 y 0 va conduce automat
la o a doua soluție de forma 0
0 și acum Haideți să discutăm despre
sisteme simetrice un sistem de
ecuații se numește Simetric dacă
este format din ecuații simetrice
Iată un exemplu de sistem Simetric
x plus y egal cu o valoare s și
x ori y egal cu p acesta este cel
mai simplu sistem Simetric și se
numește sistem Simetric fundamental
rezolvarea sistemelor simetrice
se reduce la rezolvarea a sistemului
Simetric fundamental pentru a rezolva
acest sistem vom utiliza ecuația
de gradul al doilea când se cunosc
suma și produsul rădăcinilor vom
forma Așadar o ecuație de gradul
al doilea cu necunoscuta aceasta
va fi tot pătrat minus este plus
p egal cu 0 având ca rădăcini x
și y unde este suma rădăcinilor
iar pe este produsul rădăcinilor
dacă Delta este pozitiv obținem
două soluții T1 și T2 prin urmare
soluția sistemului Simetric va
fi următoarea x egal cu 1 și y
egal cu T2 dar așa cum spuneam
mai devreme vom avea și soluția
x egal cu 2 respectiv y egal cu
1 prin urmare soluția sistemului
Simetric va fie mulțimea perechilor
de forma t1 t2 respectiv T2 T1
în continuare vom rezolvat câteva
exemple Iată un prim sistem Simetric
x plus y egal cu minus 4 și x si
y egal cu 3 observăm Așadar că
suma rădăcinilor este minus 4 iar
produsul este 3 9 forma Așadar
ecuația de gradul al doilea cu
necunoscut acte și avem te pătrat
minus este plus p f egal 0t pătrat
minus minus 4 este plus 4 plus
3 egal cu 0 Delta este b pătrat
minus patru Ace 4 la a doua minus
4 ori 1 ori 3 16 minus 12 patru
unu este minus b plus radical din
Delta supra 2-a minus 4 plus 2
pe 2 și egal cu minus unu iar T2
va fi minus 4 minus 2 supra 2 egal
cu minus 3 prin urmare sistemul
Simetric va avea soluția x egal
cu minus 1 și y egal cu minus 3
respectiv x egal cu minus trei
și y egal cu minus unu mai putem
scrie soluția sub forma aceasta
este egal mulțimea perechilor minus
1 minus 3 și minus 3 minus 1 în
al doilea exemplu avem următorul
sistem x pătrat plus pătrat egal
cu 13 și x y egal cu minus 6 în
acest caz cunoaștem produsul x
si y egal cu minus 6 însă nu cunoaștem
suma rădăcinilor va trebuie Așadar
să exprimăm această sumă x pătrat
plus y pătrat cu ajutorul sumei
x plus y pentru aceasta vom folosi
formula de calcul prescurtat x
plus y totul la pătrat egal cu
x la a doua plus y la a doua plus
2x y Deci s la pătrat va fi egal
cu x pătrat plus pătrat plus 2
pe de aici exprimăm x la a doua
plus y la a doua și obținem esti
pătrat minus 2 pe este bine să
rețineți această formulă pentru
că se va folosi destul de des în
rezolvare a sistemelor simetrice
și acum număr scrie acest sistem
cu ajutorul necunoscutelor esti
și pe prima ecuație se va scrie
s pătrat minus 2 pe egal cu 13
și pe egal cu minus 6 înlocuind
valoarea lui pi în prima ecuație
și obținem sistemul s pătrat minus
2 ori minus 6 plus 12 egal cu 13
și pe egal cu minus 6 aici avem
s pătrat egal cu unu și pe egal
cu minus 6 prima ecuație are două
soluții unu și minus unu prin urmare
acest sistem va fi echivalente
cu Reuniunea următoarelor sisteme
este egal cu 1 și pe egal cu minus
6 este egal cu minus 1 și b egal
cu minus 6 să notăm aceste sisteme
cu S1 și S2 pentru fiecare sistem
în parte vom forma ecuația de gradul
al doilea cu necunoscuta te în
cazul primului sistem avem t pătrat
minus este plus b egal cu 0 D pătrat
minus minus 6 egal cu 0 Delta este
b pătrat minus patru ace 1 minus
patru ori minus 6 și egal cu 25
unul la minus b plus radical din
Delta supra 2-a 1 plus 5 pe 2 egal
cu 3 pe 2 va fi minus b radical
din Delta supra 2-a 1 minus 5 pe
2 egal cu minus 2 de sistemul S1
va avea următoarea soluție pe care
o să notez cu S1 avem perechile
3 minus 2 și minus 2 3 acum rezolva
al doilea sistem S2 vom scrie ecuația
de gradul al doilea de pătrat minus
este plus b egal cu 0 D pătrat
plus pe minus 6 egal cu 0 Delta
va fi b pătrat minus 4 1 minus
4 ori minus 6 egal cu 25 de 1 este
minus b plus radical din Delta
supra 2-a minus 1 plus 5 pe 2 egal
cu 2 și 3 2 va fi minus 1 minus
5 supra 2 și egal cu minus 3 prin
urmare sistemul S2 va avea soluția
mulțimea perechilor 2 minus 3 și
minus 3 2 spuneam mai devreme că
sistemul inițial este echivalent
cu Uniunea celor două sisteme prin
urmare soluția finală va fi mulțimea
perechilor 3 minus 2 minus 2 3
2 minus trei și minus trei doi
și un ultim exemplu avem următorul
sistem x y plus x plus y egal cu
minus 1 și 2 x pătrat plus 2 x
pătrat minus x y egal cu 30 m să
rescriem acest sistem cu ajutorul
necunoscutelor s și p prima ecuație
va fi pe plus S egal cu minus 1
în a doua ecuație de factor comun
pe 2 avem 2 pe lângă x pătrat plus
pătrat dar x pătrat plus y pătrat
este egal cu x pătrat minus 2 pe
prin urmare în paranteză vom avea
s pătrat minus 2 pe minus b egal
cu 30 pe va fi egal cu minus 1
minus s Hai desfacem parantezele
Avem doi s pătrat minus 4 pe minus
pe este minus 5 pe minus 30 egal
cu 0 echivalent pe egal cu minus
1 minus s2s pătrat minus 5 pe lângă
minus 1 minus folosim metoda substituției
minus 30 egal cu 0 în a doua ecuație
desfacem paranteza copiem prima
ecuație pe egal cu minus 1 minus
s2s pătrat plus 5 plus 5 S minus
30 egal cu 0 este egal cu minus
1 minus s 2x pătrat plus 5s Minus
25 egal cu 0 numere zoll vă a doua
ecuație Aceasta este o ecuație
de gradul doi cu necunoscuta s
o să mai copieze încă o dată 2s
pătrat plus 5s Minus 25 egal cu
0 Delta este b pătrat Dică 5 la
a doua minus 4 ori 2 ori minus
25 egal cu 25 plus 8 ori 25 este
egal cu 200 și egal continuare
cu 225 1 este minus b plus radical
din Delta supra 2-a adică minus
5 plus radical din 225 este 15
supra 2 ori 2 egal cu 10 supra
4 și egal cu 5 pe 2 S2 va fi egal
cu minus 5 minus 15 supra 4 minus
20 supra 4 egal cu minus 5 am obținut
Așadar două valori posibile pentru
s pe este egal cu minus 1 minus
esti prin urmare vom avea pe unu
egal cu minus 1 minus 1 pe 1 va
fi minus 1 minus 5 pe 2 și egal
cu minus 7 supra 2 iar pe 2 este
minus 1 minus 2 pe 2 este egal
cu minus 1 minus minus 5 Deci plus
5 și egal cu 4 prin urmare sistemul
Simetric va fi echivalent cu Reuniunea
următoarelor sisteme f1 egal cu
5 pe doi și pe unu egal cu minus
7 supra 2 acesta va fi sistemul
S1 și al doilea sistem format din
ecuațiile F2 egal cu minus 5 și
pe 2 egal cu patru pentru fiecare
sistem în parte vom scrie ecuația
de gradul al doilea cu necunoscut
acte pătrat minus este plus p egal
cu 0 te pătrat minus 5 supra 2
minus 7 supra 2 egal cu 0 Delta
este minus 5 pe 2 la pătrat minus
4 ori minus 7 pe 2 și egal cu 2
și 5 supra 4 plus 28 pe 2 28 O2
este 56 plus 25 egal cu 81 supra
4 1 este 5 pe 2 plus radical din
Delta 9 pe 2 totul supra 2 egal
cu 14 supra 2 supra 2 adică 14
supra 4 egal cu 7 pe 2 iar cei
doi va fi egal cu 5 supra 2-a minus
nouă pe 2 totul supra 2 egal cu
minus 4 pe 4 și egal cu minus 1
bă scrie mai târziu soluția primului
sistem trecem acum la sistemul
S2 pe urmă am și aici ecuația te
pătrat minus este plus b egal cu
0 de pătrat minus minus 5 plus
500 plus 4 egal cu 0 Delta este
5 la a doua minus 4 x 4 25 minus
16 egal 9 1 este minus 5 plus radical
din 9 3 supra 2 minus 2 pe 2 minus
1 pe 2 va fi minus 5 minus 3 pe
2 minus 8 pe 2 egal minus 4 să
scriem așa dar cele două soluții
soluția sistemului S1 este mulțimea
perechilor 7 pe 2 minus unu și
minus unu șapte pe doi iar pentru
sistemul S2 avem soluția S2 mulțimea
perechilor minus 1 minus 4 și minus
4 minus 1 soluția sistemului inițial
va fi Reuniunea celor două mulțimi
și vom avea mulțimea perechilor
7 pe 2 minus 1 minus 1 7 pe 2 minus
1 minus 4 și minus 4 minus 1

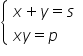
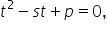 având rădăcinile
având rădăcinile