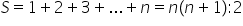Suma lui Gauss

în această secvență o să discutăm

despre ceea ce se numește suma

lui Gauss În primul rând Haideți

să vedem cine este Gauss Carl Friedrich

Gauss a fost un mare matematician

german care sa remarcat încă din

copilărie prin faptul că făcea

calcule foarte rapid și corect

se spune că în timpul unei ore

de matematică pentru că mereu termina

foarte repede ce avea de rezolvat

învățătorul său ia dat să calculeze

următoarea suma 1 plus 2 plus 3

plus și așa mai departe până la

100 gândind usei că o asemenea

sumă o să îi dea ceva de lucru

micului Gauss însă ce credeți nu

a fost așa și gauza calculat foarte

repede această sumă cum a făcut

acest lucru pe el a observat că

dacă adună primul număr cu ultimul

în cazul nostru pe unu cu 100 obține

suma 101 dacă la adună pe 2 cu

numărul din fața lui Care este

99 și în fața lui avem și 98 Deci

adunând ul pe 2 cu 99 obține tot

101 dacă la adună mai departe pe

3 cam 98 din nou obține 101 și

așa mai departe De ce la observat

că întotdeauna grupând termenii

2 câte 2 va obține numărul 101

Întrebarea este de câte ori ne

apare 101 Păi Câte grupe avem noi

avem în total 100 de numere și

le grupăm două câte două pe asta

înseamnă că 100 împărțit la 2 ne

dă 50 Deci avem 50 de grupe cu

alte cuvinte numărul 101 apare

de 50 de ori Deci venim aici scriem

egal mai departe cu 101 apare de

50 de ori Deci îl înmulțim cu 50

și rezultatul este putem Să considerăm

așa 101 ori 5 ori 10 face mai întâi

acest produs și ne dă 505 ușor

de văzut și apoi adăugăm 0 de la

final prin înmulțirea cu 10 cu

alte cuvinte Rezultatul este 5050

și atât ca astfel la calculat foarte

rapid Gauss această sumă e bine

o sumă de numere consecutive cum

avem aici de numere naturale consecutive

poartă numele de suma lui Gauss

și acum Haideți înainte să trecem

la un alt exemplu să vedem ce numere

regăsim de fapt aici în mijloc

pentru că Iată după 3:00 o să urmeze

patru care se va aduna cu 97 bun

însă Ce numere vom regăsi în mijloc

adică ce numere consecutive adunate

au suma 101 pe las puțin timp să

vă gândiți vorbim de numerele 50

și 51 Deci aici avem din nou puncte

de suspensie și avem plus 97 la

fel aici 4 plus și puncte de suspensie

Iată 50 adunat cu 51 și acestei

două numere au suma 100 Haideți

să facem acum alt exemplu și pentru

că aici am avut un număr par de

numere 1 acum un număr impar de

numere Deci vrem să calculăm suma

numerelor 1 plus 2 plus 3 plus

și așa mai departe și Vrem un număr

impar să mergem până la 21 nu luăm

un număr foarte mare Cum procedăm

ideea e ca mai înainte Deci vomă

adunat primul număr cu ultimul

1 cu 21 și obținem 22 apoi pe 2

cu cât îl adunăm Haide să scriem

aici avem 20 Pardon Și aici avem

19 deci pe 2 îl vom aduna cu 28

Ne tot 22 pe trei îl adunăm cu

19 cât obținem deja nu vă mai surprinde

tot 22 și așa mai departe cu alta

cuvinte noi obținem suma an ținem

acest număr 22 însă problema care

apare aici este aceea că noi avem

în total 21 de numere adică avem

un număr impar de numere și de

vreme ce noile grupăm două câte

două Da Ce înseamnă înseamnă că

o să fie un număr care nu are pereche

care este acel număr Păi Haideți

să ne gândim puțin ca să obținem

suma 22 noi la un moment dat vom

avea pe 10 pe care îl vom aduna

cu cât Păi la adunăm cu 12 și ne

dă 22 Haide să trecem semnele plus

și plus Deci îl adun pe 10 cu 12

și vom obține 22 și o să ne mai

rămână Iată numărul 11 care rămâne

fără pereche în această situație

Cum calculăm suma noastră Păi Haideți

să gândim așa Noi avem numerele

să scriem cu altă culoare avem

numerele 1 2 3 și așa mai departe

10 11 12 19 20 21 mai avem 21 de

numere pe 11 îl dăm afară știm

cu el rămâne fără pereche câte

numere ne rămân pâine rămân dacă

din 21 dăm afară unul ne rămân

20 de numere 20 de numere dat pe

care le grupăm Iată două câte două

Deci avem 20 împărțit la 2 cu alte

cuvinte 10 grupe având 10 grupe

înseamnă că numărul 22 apare de

10 ori aici nu prea pare că am

scris Group Deci avem 10 Group

și acum venim și terminăm calculul

nostru va fi egal cu numărul 22

apare de 10 ori Deci 22 înmulțit

cu 10 plus numărul 11 care nu are

pereche deci 220 adunat cu 11 obținem

231 și aceasta este suma pe care

am obținut o ia ataca atunci când

avem numere un număr impar de numere

Adică când ultimul număr este impar

și avem o sumă de numere consecutive

începând de la unu în lucrurile

par puțin mai complicate dacă vi

se pare mai complicat cel puțin

Mie așa mi sa părut când mi sa

arătat această metodă și eram cam

de vârsta voastră 10 11 ani putem

să facem și altfel și cum procedam

deci încă o metodă vrem să calculăm

această sumă ori scrie Deci până

la 21 Da 1 plus 2 plus 3 plus și

așa mai departe Plus 21 bun această

sumă Haide să notăm cu o literă

și o notez cu s de la suma aceeași

sumă Deci tot suma s o Vom Rescrie

altfel în ordinea descrescătoare

a termenilor adică începem de la

21 21 plus 20 plus 19 plus și așa

mai departe Haide să trecem și

aici 1920 ca să vedeți clar și

aici vom avea trei plus doi plus

unu ce vom face în continuare este

faptul că vom aduna aceste două

relații Iată și folosim această

notație și să rețineți că întotdeauna

putem să adunăm două egalități

și ca să vă fie mai clar o să luăm

un exemplu mai simplu Să considerăm

că ei așa am notat noi suma este

reprezintă 1 plus 3 și b am notat

cu altă literă 2 plus S9 și vrem

să facem suma a plus b Păi punem

aici operația de adunare Ce înseamnă

că în sumă munceste două relații

înseamnă că vom adunat membrii

care se află înaintea egalului

deci a plus b trecem apoi egalul

că am ajuns în dreptul lui și apoi

adunăm membri care se află după

egal Deci 1 plus 3 adunat cu 2

plus 9 și rezultatul Cât este avem

15 bun acum având aici și în adunare

știind că noi putem să adunăm termenii

în orice ordine dorim fiind peste

tot o operație de adunare și știm

că folosind proprietățile adunării

asta înseamnă că poți să aduni

de exemplu pe unul cu doi mai întâi

și apoi pe 3 cu 9 adică Iată pe

unul îl adun cu doi Deci suma a

plus b o putem scrie direct și

așa unul adunat cu 2 care ne dă

3 plus Haideți să scriem acest

pus mai jos plus pe trei la Dancu

nouă și îmi dă 12 și atât Că Rezultatul

este 3 Cu 12 tot 15 deci putem

să facem suma și astfel așa o să

procedăm și pentru suma dată înseamnă

tot cu S mare Deci și calculăm

am scris cu albastru S plus S Deci

notăm i s adunat cu s y este egal

cu Ce facem acum suma 1 plus 21

adică 22 plus 2 cu 2022 plus 3

cu 19 tot 22 plus și așa mai departe

aici deja nu mai sunteți surprinși

22 din nou 22 din nou 22 Întrebarea

este acum Câte 22 avem Păi Haideți

să ne uităm puțin când îl adunăm

pe unul cu 21 Deci făcând această

sumă am o primul 22 făcând această

sumă la am obținut pe al doilea

22 această sumă de la dat pe al

treilea 22 de fapt aceste numere

1 2 și 3 și așa mai departe se

comportă ca niște contoare de numărare

Ele ne arată Care este poziția

lui 22 sau de câte ori apare 22

făcând această sumă 21 cu 1 milă

dat de fapt de 21-lea 22 de ceartă

că 22 apare de fapt de 21 de ori

Deci venim și noi aici și notăm

21 înmulțit cu 22 S plus S îl putem

scrie doi orez și s este egal cu

avem 21 ori 22 împărțit la doi

și rezultatul O să vedeți că o

să vă dea 231 iar 231 am obținut

și aici mie când era mică Mi se

apărut mai simplă această metodă

și acum Haideți să generalizăm

cu alte cuvinte dacă avem de calculat

această sumă 1 plus 2 plus 3 plus

și așa mai departe plus n unde

n este un număr natural mai mare

decât 1 Care este formula pentru

suma lui Gauss Păi Haideți să ne

închipuim că în locul lui 21 am

avea de fapt an si vom scrie atunci

din acest pas de la acest pas mă

refer apoi vom obține așa 2 ori

esti 2 ori esti va fi egal cu un

loc de 21 scris am zis că scrie

m n e n înmulțit cu ce trecem în

loc de 22 n plus 1 n plus 1 și

a venit sa trecem în paranteză

Deci îți va fi and înmulțit cu

n plus 1 împărțit la doi Deci nu

împărțit la doi Ei chiar aceasta

este și formula notăm aici e n

înmulțit cu n plus 1 împărțit la

2 oricare ar fi n număr natural

valabil această formulă și să ai

de Să scriem aici că avem de a

face cu formula pentru suma lui

Gauss Deci notăm suma lui Gauss

acum ce am făcut aici nu este o

demonstrație este o analogie Dacă

voi chiar vrei să faceți demonstrația

pentru această formulă atunci puteți

să luați suma 1 plus 2 plus 3 plus

și așa mai departe plus n și procedați

exact ca aici O să vedeți că obțineți

această formulă Acum ne este de

folos să reținem o asemenea formulă

sigur cu ajutorul ei putem să calculăm

foarte rapid asemenea sume de numere

consecutive indiferent dacă n este

număr par sau impar Iată aceasta

este formula și acum Haideți să

facem și două exemple vrem să calculăm

valoarea acestei sume 1 plus 2

plus 3 plus și așa mai departe

și haide să caut un număr să fie

par de exemplu 34 egal cu Cum procedăm

Păi ne uităm la formulă Ia de aici

ne apare în formulă an la noi n

este 34 Deci în loc de en scrie

m34 înmulțit cu în loc de n plus

1 vom avea 34 plus 1 totul împărțit

la 2 Și acum facem calculul avem

34 ori aici obținem 35 împărțit

la 2 Acum mai târziu o să discutăm

că înmulțirea este și a comutativă

ca și adunarea adică Putem să schimbăm

locul acestor doi factori și vom

avea 35 înmulțit cu 34 împărțit

la 2 De ce ne este de folos această

schimbare de poziție a factorilor

Pentru că atunci când avem o înmulțire

urmată de o împărțire putem să

facem mai întâi împărțirea egal

cu 35 înmulțit cu aici obținem

17 și avem de calculat acest produs

care ne dă 595 bun să luăm acuma

text Samp luni care an să nu fie

par atunci să fie cum să fie impar

și avem 1 plus 2 plus 3 plus și

mergem până la 47 egal cu Aplicând

formula în loc de en scriem 47

înmulțit cu 40 și 7 plus 1 împărțit

la 2 și vom avea așa 47 ori 48

împărțit la 2 ce credeți că facem

acum face mai întâi această înmulțire

sau împărțire apoi face mai întâi

împărțirea pentru că vom obține

aici un număr mai mic Deci avem

47 ori 24 și la acest produs care

duce calculul nostru rezultatul

e 1.128 iar dacă dacă știm această

formulă putem să calculăm foarte

rapid asemenea sumei indiferent

dacă n este număr par sau impar