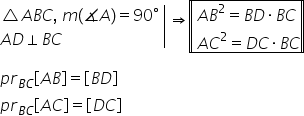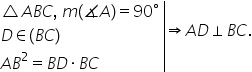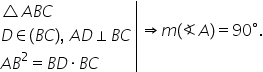Teorema catetei

teorema catetei intru în triunghi

dreptunghic lungimea unei catete

este media geometrică a lungimii

ipotenuzei și a lungimii proiecției

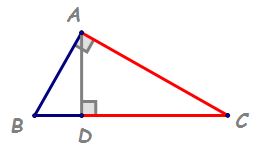
sale pe ipotenuză avem un triunghi

dreptunghic ABC cu măsura unghiului

A de 90 de grade în acest triunghi

catetele sunt ab și ac iar BC este

ipotenuza am zis de asemenea o

perpendiculară a D pe latura b

c proiecția catetei ab pe ipotenuză

este BD iar proiecția catetei AC

pe ipotenuză este de ce atunci

conform teoremei catetei a b la

pătrat va fi egal cu bd ori bc

și ac la pătrat este egal cu DC

ad bc în demonstrația stă teoremă

ne propunem Să arătăm că triunghiul

adb este asemenea cu triunghiul

c ab Nu am folosit primul caz de

asemănare și vom demonstra ca aceste

triunghiuri au două unghiuri respectiv

congruente în primul rând observăm

că cele două triunghiuri sunt dreptunghice

așa dar unghiul adb va fi congruent

cu unghiul bac pentru că acestea

au măsura egală cu 90 de grade

putem observa că unghiul b din

triunghiul adb este congruent cu

unghiul b din triunghiul c ab adică

unghiul b este un unghi comun unghiul

ABD este congruent cu unghiul abc

din aceste două relații va rezulta

conform primului caz de asemănare

că triunghiul adb este asemenea

cu triunghiul c ab bine la cea

de asemănare a celor două triunghiuri

va rezulta o relație de proporționalitate

între laturile acestora ne uităm

mai întâi În triunghiul adb latura

care se opune unghiului B în acest

triunghi este ad iar latura care

se opune unghiului b din triunghiul

mare este ac în triunghiul adb

latura care se opune unghiului

drept ia sta ab iar în triunghiul

mare ipotenuza este bc din primul

triunghi a mai rămas latura b d

iar din triunghiuri mare a mai

rămas latura ab în continuare vom

folosi egalitatea dintre ultimele

două rapoarte înmulțim pe diagonală

și obținem că ab ori ab este egal

cu bd ori b c dar a b ori ab este

ab la pătrat egal cu bd ori bc

am demonstrat astfel prima relație

în mod Analog se demonstrează și

cea de a doua relație nu voi mai

face și această demonstrație această

teoremă are două teoreme reciproce

prima reciprocă fie un triunghi

abc cu măsura unghiului A de 90

de grade și d un punct situat pe

latura bc Dacă AB la pătrat este

egal cu bd ori bc atunci va rezulta

că AD este perpendiculară pe BC

și cea de a doua teoremă reciprocă

Fie abc un triunghi și d un punct

situat pe latura bc ad înălțime

în acest triunghi dacă a b la pătrat

este egal cu bd ori bc atunci măsura

unghiului a va fi egală cu 90 de

grade cu alte cuvinte triunghiul

va fi dreptunghic în continuare

o să facem o aplicație avem următoarea

problemă Fie abc un triunghi dreptunghic

în A și AD perpendiculară pe BC

Se știe că bc este egal cu 25 centimetri

și BC egal cu 16 cm se cere să

calculăm lungimea segmentelor BD

AB AC și AD mai întâi vom afla

lungimea segmentului BD observăm

că b d este egal cu b c minus d

c egal cu 25 minus 16 și egal cu

9 cm mai scrie și pe figură b d

egal cu 9 pentru a afla lungimea

catetei ab o să aplicăm teorema

catetei din teorema catetei va

rezulta că ab la pătrat este egal

cu bd ori b c a b la pătrat va

fi egal cu 9 ori 25 a b la pătrat

egal cu 225 abe va fi radical din

225 și obținem că ab este egal

cu 15 cm acum Trebuie să aflăm

lungimea catetei ac conform teoremei

catetei AC la pătrat este egal

cu DC ori b c acela pătrat va fi

egal cu 16 ori 25 având numere

că 16:25 sunt pătrate perfecte

Nu este neapărat necesar să efectuăm

acest produs putem aplica reguli

de calcul cu radical a ce va fi

egal cu radical din 16 ori 25 egal

în continuare cu radical din 16

ori radical din 25 radical din

16 este 4 și radical din 25 este

5-a si va fi egal cu 20 ac egal

cu 20 cm și pentru a afla lungimea

înălțimii ad aplicăm teorema înălțimii

din teoremă înălțimii rezultă că

a d la pătrat este egal cu bd ori

de ce Adela pătrat este egal cu

9 ori 16 avem din nou două pătrate

perfecte 9 și 16 și atunci nu e

necesar să facem înmulțirea a da

fie egal cu radical din 9 ori 16

egal cu radical din 9 ori radical

din 16 egal cu 3 ori 4 și egal

cu 12 ad egal cu 12 cm