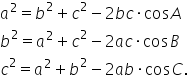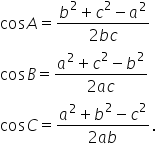Teorema cosinusului
Tag-uri
Partajeaza in Google Classroom
Transcript
în geometrie plană elementele pe
care trebuie să le calculăm nu
se află în general în triunghiuri
dreptunghice de aceea trebuie studiate
relațiile dintre unghiurile și
laturile unui triunghi oarecare
cele mai importante relații sunt
cele din teorema cosinusului și
teorema sinusurilor teorema cosinusului
ne ajută să calculăm una din Laturile
unui triunghi Cunoscând celelalte
două laturi și unghiul dintre acestea
sau putem calcula unghiurile triunghiului
Cunoscând cele trei laturi avem
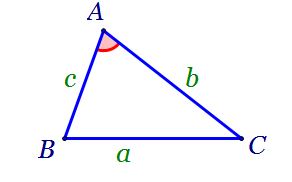
un triunghi oarecare abc am tot
cu a mic latura opusă unghiului
A cu b mic latura opusă unghiului
b și cu c mic latura opusă unghiului
c atunci au loc următoarele relații
dintre ma cosinusului a la pătrat
este egal cu b la pătrat plus c
la pătrat minus 2 b c ori cosinus
de a b la pătrat este egal cu a
pătrat plus c pătrat minus 2 AC
ori cosinus de b iar c la pătrat
este egal cu a la pătrat plus b
la pătrat minus 2ab ori cosinus
de C vom demonstra prima relație
celelalte tratând duce analog În
triunghiul abc are loc următoarea
relație vectorială vectorul BC
este egal cu AC minus ab să scriem
această relație Deci BC este egal
cu AC minus AB Dacă ridicăm la
pătrat această relație obținem
bc la pătrat egal cu AC minus ab
la pătrat și egal cu AC la a doua
minus 2 ace ori ab plus ab la pătrat
b c sau notat cu a mic deci a la
a doua este egal ac se notat cu
b mic plus a b la pătrat este si
la pătrat minus 2 ori aici avem
produsul scalar dintre vectorii
ac și ab Haideți să calculăm AC
ori ab avem modul de a c ori modul
de a b ori cosinusul unghiului
dintre vectorii AB și AC adică
cosinus de a și egal cu b ori c
ori cosinus de a Revenim la relația
de mai sus și în loc de ace ori
ab avem bc ori cosinus de ei am
demonstrat Așadar prima relație
din teorema cosinusului celelalte
două relații se demonstrează analog
mămica observație Aș vrea să facem
în cazul în care măsura unghiului
a este egală cu 90 de grade Deci
avem un triunghi dreptunghic atunci
cosinus de a este 0 prin urmare
acest termen 2bc ori curs de a
se anulează iar teorema se va scrie
a la pătrat egal cu b la pătrat
plus si la pătrat obținem astfel
chiar teorema lui Pitagora din
acest motiv teorema cosinusului
mai poartă denumirea de teorema
lui Pitagora generalizată din aceste
trei relații putem să exprimăm
cosinus de a cosinus de b și cosinus
de c și obținem următoarele formule
cos de a este egal cu b la pătrat
plus c la pătrat minus a la pătrat
supra 2 bc cosinus de B este a
la pătrat plus c la pătrat minus
b pătrat supra 2-a c iar cosinus
de c este a pătrat plus b pătrat
minus c pătrat supra 2 ab aceste
formule ne permit să calculăm unghiurile
triunghiului ABC Cunoscând lungimile
laturilor acestuia Haideți să facem
în continuare un exercițiu avem
triunghiul abc în care lungimea
segmentului AB este de 5 unități
lungimea segmentului ac este de
șapte unități Se știe că măsura
unghiului a este egală cu 60 de
grade și se cere să calculăm perimetrul
triunghiului ABC pentru a calcula
perimetrul triunghiului ABC trebuie
să calculăm mai întâi lungimea
laturii BC aplicăm teorema cosinusului
și avem bc la pătrat egal cu AB
la pătrat plus AC la pătrat minus
2ab ori AC ori cosinus de Deci
bc la a doua va fi egal cu 5 la
pătrat adică 25 plus 7 la a doua
49 minus 2 ori cinci ori șapte
ori cosinus de 60 Adică 1 pe 2
25 plus 49 este 74 minus 5 ori
735 obținem 39 prin urmare b c
la final cu radical din 39 și acum
putem calcula perimetrul triunghiului
ABC va fi 5 plus 7 plus radical
din 39 și obținem în final 12 plus
radical din 39
Teorema cosinusuluiAscunde teorie X
Navigare în lectii
Cumpara abonament
