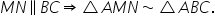Teorema fundamentală a asemănării (teorie)

în această lecție o să discutăm

despre teorema fundamentală a asemănării

aceasta are următorul enunț o paralelă

la una din Laturile unui triunghi

formează cu celelalte două laturi

sau cu prelungirile lor un triunghi

asemenea cu cel dat avem un triunghi

abc și m n duce o paralelă la dreapta

BC pe care am notat cu de în acest

caz îmi spune că triunghiul a d

e este asemenea cu triunghiul abc

după cum Observați Există trei

posibilități în primul caz dreapta

d e este în interiorul triunghiului

ABC iar în celelalte două cazuri

dreapta d intersectează prelungirile

laturilor triunghiului abc în fiecare

dintre cele trei situații triunghiul

a d e este asemenea cu triunghiul

ABC mă face demonstrația aceste

teoreme în primul caz celelalte

cazuri tratând USA analog avem

triunghiul abc și am zis dreapta

d e paralelă cu bc trebuie să arătăm

că triunghiul a d e este asemenea

cu triunghiul abc Maria amintesc

că două triunghiuri sunt asemenea

dacă au toate cele trei unghiuri

respectiv congruente și laturile

proporționale ne uităm mai întâi

la unghiuri Dacă dreapta d este

paralelă cu bc iar ab este secantă

atunci unghiurile ad și abc vor

fi unghiuri congruente pentru că

acestea sunt unghiuri corespondente

unghiul ad va fie congruent cu

unghiul abc fiind unghiuri corespondente

apoi unghiurile a e d și ACB vor

fi și acesteia congruente unghiul

A e d congruent cu unghiul ACB

din și acesteia unghiuri corespondente

iar unghiul A este un unghi comun

al celor două triunghiuri putem

scrie că unghiul A este congruent

cu unghiul a fiind un unghi comun

am arătat că cele trei unghiuri

sunt respectiv congruente pentru

a arăta că triunghiurile sunt asemenea

mai trebuie să demonstrăm că laturile

acestora sunt proporționale Dacă

d este paralelă cu bc putem aplica

teorema lui Thales care ne spune

că o paralelă dusă la una din Laturile

unui triunghi formează cu celelalte

două laturi segmente proporționale

am văzut în lecția respectivă că

folosind proporții derivate putem

scrie următoarea egalitate de rapoarte

ad supra ab este egal cu AE supra

ac avem astfel o egalitate între

două rapoarte mai trebuie doar

să arătăm că raportul a supra AC

este egal cu d e supra bc pentru

a finaliza această demonstrație

să vedem cum putem demonstra în

continuare egalitatea acestor două

rapoarte pentru aceasta vom face

o construcție ajutătoare și o să

ducem prin punctul E o paralelă

la latura ab fie e paralelă cu

AB observăm că aici sa format un

paralelogram de e f b este paralelogram

pentru că are laturile paralele

două câte două Și de aici A rezultat

că de e este egală cu bere dacă

e f este paralelă cu AB putem aplica

din nou teorema lui Thales pe care

o scris sub următoarea formă a

supra AC este egal cu BF supra

bc însă b e f este egal cu d e

și atunci va rezulta că a e supra

ac este egal cu d e supra bc am

demonstrat Așadar această relație

din relațiile 1 și 2 va rezulta

că laturile celor două triunghiuri

sunt proporționale a d supra ab

este egal cu AE supra ac și egal

cu d e supra bc și de aici va rezulta

că triunghiul a d e este asemenea

cu triunghiul abc observăm că teorema

fundamentală a asemănării Completează

teorema lui tales deoarece Concluzia

este mai cuprinzătoare aceasta

referindu sta la toate cele trei

laturi ale triunghiurilor