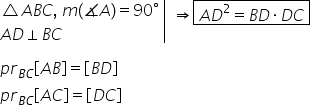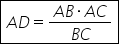Teorema înălțimii- aplicații

rezolvăm în continuare o problemă

în care o să aplicăm cele două

teoreme pe care le am învățat mai

devreme triunghiul dreptunghic

ABC are ipotenuza BC egală cu 20

cm iar raportul dintre lungimile

proiecțiilor catetelor pe ipotenuză

este 4 Calculați lungimea înălțimii

corespunzătoare ipotenuzei iar

la punctul b dacă ab este ogradă

cal din 5 Calculați lungimea catetei

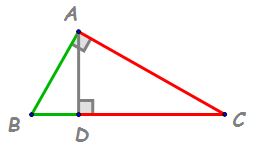
ac observăm că triunghiul ABC este

dreptunghic în A iar înălțimea

corespunzătoare ipotenuzei este

ad unde AD este perpendiculară

pe b c proiecția catetei ab pe

ipotenuză este în BD iar proiecția

catetei AC pe ipotenuză este de

c pentru a redacta mai simplu rezolvarea

acestei probleme o să notăm lungimea

segmentului BD cu x și lungimea

segmentului DC cu y din problema

că Raportul proiecțiilor catetelor

este 4 Prin urmare avem următoarea

relație x supra y este egal cu

4 b c are 20 cm și observăm că

bc este egal cu x plus y deci putem

să scriem și această relație între

x și y o să scriu aici x plus y

este egal cu 20 Avem două relații

cu două necunoscute pentru a calcula

lungimea înălțimii ad mai întâi

trebuie să calculăm valoarea lui

x și y din prima proporție o să

le exprimăm pe x înmulțim pe diagonală

x va fi egal cu 4 x y și acum înlocuind

pe x în a doua egalitate astfel

din cele două relații obținem că

4 y plus y este egal cu 25 x este

egal cu 20 m astfel o ecuație cu

necunoscuta y1 ecuația la 5 va

fi egal cu 4 lungimea segmentului

d c este 4 cm acum să aflăm și

lungimea segmentului bd dacă x

este egal cu 4 y ma rezultat că

x este egal cu 4 ori 4 și egal

cu 16 cm Deci b d are lungimea

egală cu 16 cm am arătat că de

ce este egal cu 4 cm și BD este

egal cu 16 cm Acum putem să calculăm

lungimea înălțimii ad folosind

prima teoremă pe care am văzut

o mai devreme a de la pătrat este

egal cu bd ori de ce Adela pătrat

este egal cu 16 ori 4 Adela pătrat

este egal cu 64 de unde rezultă

că ab este egal cu radical din

64 și egal cu 8 cm am terminat

cu punctul A trecem la punctul

b dacă ab este 8 radical din 5

Calculați lungimea catetei ac pentru

aceasta o să folosim a doua teoremă

pe care am demonstrat în mai devreme

și anume Ade este egal cu raportul

dintre produsul catetelor și ipotenuză

a b ori a c supra b c înlocuim

în această relație segmentele cunoscute

a d este egal cu 8 AB este 8 radical

din 5 ori ace supra 20 din această

egalitate trebuie să îl aflăm pe

a ce avem astfel o proporție o

să înmulțim pe diagonală și obținem

că opt ori 20 este egal 8 radical

din 5 ori ace observăm că factorul

opt apare și în membrul stâng și

în membrul Drept deci putem să

împărțim egalitatea la 8 și obținem

că 20 este egal cu radical din

5 ori AC împărțim la radical din

5 a ce va fi egal cu 20 supra radical

din 5 putem să raționalizăm acela

fie egal cu 20 radical din 5 supra

5 se simplifică în 20 cu 5 și ne

rămâne 4 prin urmare a ce va fi

egal cu patru radical din 5 cm