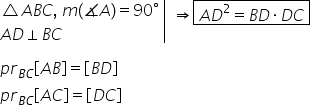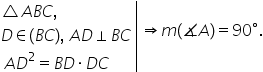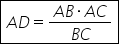Teorema înălţimii (teorie)
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să învățăm
teoremă înălțimii în triunghi dreptunghic
dar mai întâi aș vrea să vă reamintesc
o noțiune învățată la algebră și
anume media geometrică a două numere
dacă avem două numere pozitive
a și b atunci media geometrică
a acestor două numere este radical
din produsul lor dacă ridicăm la
pătrat această egalitate obținem
că media geometrică la pătrat este
egală cu a ori b media geometrică
se mai numește și media proporțională
a numerelor a și b și acum putem
să enunță teorema înălțimii Într
un triunghi dreptunghic lungimea
înălțimii corespunzătoare ipotenuzei
este media geometrică a lungimilor
proiecțiilor catetelor pe ipotenuză
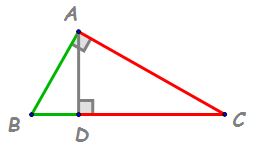
avem un triunghi dreptunghic ABC
și am duce înălțimea AD corespunzătoare
ipotenuzei BC proiecțiile catetelor
pe ipotenuză sunt bd și DC atunci
Adela pătrat va fi egal cu bd ori
de ce o să demonstrăm această teoremă
nu mă arăta că triunghiul ABD este
asemenea cu triunghiul c a d pentru
că nu avem nici o informație referitoare
la lungimile laturilor acestor
două triunghiuri mama arăta că
ele sunt asemenea conform primului
caz de asemănare și vom demonstra
că aceste triunghiuri au două unghiuri
respectiv congruente Așadar ne
propunem Să arătăm că triunghiul
ABD este asemenea cu triunghiul
c a d observăm că acestea sunt
triunghiuri dreptunghice Deci o
pereche de unghiuri congruente
ar fi unghiurile adb și adc deoarece
acestea sunt unghiuri drepte unghiul
adb este congruent cu unghiul adc
pentru că acestea au măsura egală
cu 90 de grade nu mai uita în continuare
că unghiul ABD este congruent cu
unghiul c a d știind că în triunghiul
abc suma măsurilor unghiurilor
sale este de 180 de grade deci
putem să scriem că măsura unghiului
a plus măsura unghiului B plus
măsura unghiului c este egală cu
180 de grade măsura unghiului a
este de 90 de grade deci putem
să scriem 90 de grade plus măsura
unghiului b plus măsura unghiului
c este egală cu 180 de grade de
aici va rezulta că măsura unghiului
B plus măsura unghiului c va fi
egală cu 180 de grade minus 90
adică 90 de grade de unde va rezulta
că măsura unghiului B este egală
cu 90 de grade minus măsura unghiului
c notam această relație cu unu
acum să ne uităm În triunghiul
a b c și în acest triunghi suma
măsurilor este de 180 de grade
o scrie că măsura unghiului adc
plus măsura unghiului d a c toți
măsura unghiului c este egală cu
180 de grade măsura unghiului adc
este de 90 de grade 90 plus măsura
unghiului d a c plus măsura unghiului
c va fi egală cu 180 de grade de
aici va rezulta că măsura unghiului
dac plus măsura unghiului c este
egală cu 180 minus 90 egal cu 90
de grade exprimăm din această relație
măsura unghiului dac aceasta va
fi egală cu 90 de grade minus măsura
unghiului c uitam această relație
cu doi din relațiile 1 și 2 Putem
afirma că unghiul b adică unghiul
ABD este congruent cu unghiul dac
deoarece aceste două unghiuri au
același complement din relația
1 și relația 2 rezultă că unghiul
ABD este congruent cu unghiul de
ac pentru ca au același complement
am arătat astfel că cele două triunghiuri
a b d și c a d a două unghiuri
respectiv congruente și atunci
va rezulta conform primului caz
de asemănare că triunghiurile ABD
și ce a d sunt triunghiuri asemenea
putem să tăiem semnul întrebării
din relația de asemănare a celor
două triunghiuri va rezulta o relație
de proportionalitate dintre laturile
acestora trebuie să fim atenți
atunci când scriem egalitatea rapoartelor
întotdeauna la numărători o să
avem laturi ale triunghiului ABD
iar la numitor o să avem laturile
triunghiului si ad cu triunghiul
ABD și cum scrie de exemplu latura
care se opune unghiului drept din
triunghiul adb aceasta este ab
supra latura care se opune unghiului
drept din triunghiul c a d aceasta
este AC acum în primul triunghi
vom scrie latura care se opune
unghiului B aceasta este Ade iar
în al doilea triunghi are latura
care se opune unghiului congruent
cu unghiul b și anume latura opusă
unghiului c a d aceasta este de
ce și acum îmi scrii laturile care
au mai rămas în triunghiul ABD
a mai rămas latura BD ia din triunghiul
c a d a mai rămas latura ad sau
ne putem gândi și altfel Putem
să scriem cea mai mare latură din
primul triunghi supra cea mai mare
latură din al doilea triunghi egal
cu cea mai mică latură din primul
triunghi supra cea mai mică latură
din al doilea triunghi și așa mai
departe am obținut astfel un șir
de rapoarte egale din această relație
nu folosit doar egalitatea dintre
ultimele două rapoarte având în
vedere că avem o proporție putem
egala produsul mezilor cu produsul
extremilor astfel obținem a de
ori a d egal cu bd ori de ce dar
Ade ori Ade este a de la pătrat
egal cu bd ori de ce am arătat
astfel că nu intru în triunghi
dreptunghic înălțimea corespunzătoare
ipotenuzei este media geometrică
a proiecțiilor catetelor pe ipotenuză
este valabilă și reciproca acestei
teoreme fie un triunghi abc și
d un punct situat pe latura bc
astfel încât ad să fie perpendiculară
pe bc adică ad este înălțime și
a de la pătrat este egal cu bd
ori De ce atunci măsura unghiului
a este egală cu 90 de grade Deci
triunghiul va fi dreptunghic o
altă teoremă teorema 2 care se
mai numește și a doua teoremă a
înălțimii în triunghi dreptunghic
înălțimea corespunzătoare ipotenuzei
este egală cu raportul dintre produsul
catetelor și ipotenuza dacă avem
un triunghi dreptunghic ABC cu
măsura unghiului A de 90 de grade
și am dus înălțimea AD atunci ad
va fi egal cu AB AC supra bc unde
mustră această teoremă scrie aria
triunghiului ABC în două moduri
mai întâi aria triunghiului ABC
poate fi scrisă ca produsul dintre
bază de ce ori înălțimea a d supra
2 Dar aria triunghiului ABC se
mai poate scrie și produsul catetelor
supra 2 având în vedere că acesta
este un triunghi dreptunghic astfel
putem considera baza latura ab
iar înălțimea corespunzătoare a
cealaltă catetă a c aria triunghiului
se mai scrie a b ori a c supra
2 putem să egalăm cele două arii
și a rezultat că bc ori ad supra
2 este egal cu a b ori a c supra
2 înmulțim toate egalitatea cu
2 și obținem că bc ori este egal
cu AB ori ac ca să ne aflăm pe
a d o să împărțim această egalitate
la b c și obținem că AD este egal
cu AB ori ace supra bc rețineți
și această formulă înălțimea în
triunghi dreptunghic se poate scrie
a raportul dintre produsul celor
două catete și ipotenuze în continuare
o să facem o aplicație aia monitoare
a problemă Se dă un triunghi ABC
dreptunghic cu măsura unghiului
A de 90 de grade ad este perpendiculară
pe bc ad este egal cu 12 cm și
CD este egal cu 8 cm se cere să
calculăm lungimea segmentelor BD
și BC având în vedere că ad este
înălțime În triunghiul dreptunghic
ABC putem să aplicăm prima teoremă
pe care am văzut în această lecție
AD este perpendiculară pe BC și
atunci va rezulta că a de la pătrat
este egal cu bd ori de ce Adi este
1212 la pătrat egal cu bd ori 8
12 la a doua este 144 egal cu bd
ori 8 pentru a afla lungimea segmentului
BD împărțim această egalitate la
8 144 împărțit la 8 este 18 egal
cu bd altfel scris BD este egal
cu 18 și acum pentru a afla lungimea
segmentului BC o să adunăm segmentele
bd și DC De ce va fi egal cu bd
plus bc egal cu 18 plus 8 și egal
cu 26 cm