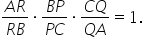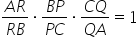Teorema lui Ceva (teorie)

Giovanni ceva A fost un matematician

italian iar reciproca teoremei

Ce poartă numele este un instrument

util în studiul concurenței unor

drepte să vedem mai întâi enunțul

teoremei lui ceva fie un triunghi

abc și punctele p q r pe situat

pe latura bc q situat pe latura

ac și f situat pe latura AB Dacă

dreptele a p b q și c f sunt concurente

atunci are locul următoarea relație

aer supra rb ori b p supra Pepsi

orice q supra Q A este egal cu

1 O dreaptă care trece prin vârful

unui triunghi se numește sibiană

Așadar dreptele AP BQ și CF se

numesc cei vienei pentru a demonstra

această teoremă o să aplicăm teorema

lui menelaus mai întâi aplicăm

teorema lui menelaus În triunghiul

a b p cu transversala a r m c Haideți

să evidențiem mai clar acest triunghi

Așadar triunghiul abp cu transversala

rmc și vom avea aer supra rb ori

b c supra CP ori m supra m a egal

cu unu Deci aer supra r b ori b

c supra CP ori pe m supra m a egal

cu 1 notăm această relație cu unu

în continuare aplicăm teorema lui

menelaus în alt triunghi mai exact

în triunghiul abc cu transversala

b m q și o să avem a m supra mp

ori pe b supra bc orice q supra

q a egal cu unu a m supra mp ori

pe b supra b c orice q supra a

egal cu unu notăm cu doi această

relație și acum înmulțim relațiile

1 și 2 membru cu membru din relațiile

1 și 2 o să avem aer supra b ori

b c supra CP ori pe m supra m a

ori a m supra mp ori pe b supra

bc orice q supra q a egal cu unu

se simplifică m a cu a m pe m cu

m p și b c cu b c și acum să vedem

cine a rămas avem aer supra airbag

ori pe b supra CP ori c q supra

a egal cu 1 iar aceasta este chiar

relația din teorema lui ceva așa

dar am demonstrat această teoremă

iar în continuare să vedem reciproca

teoremei lui ceva fie un triunghi

abc și punctele p q r astfel încât

p să fie situat pe latura b c q

să fie situat pe latura AC și R

situat pe latura ab dacă are loc

relația aer supra erbe ori b p

supra p c orice q supra Q A egal

cu 1 atunci ce vinele a p q și

R sunt concurente folosind reciproca

teoremei lui ceva se poate demonstra

concurența unor linii importante

în triunghi iar în secvența următoare

o să demonstrăm concurență a medianelor