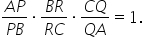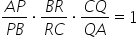Teorema lui Menelaus (teorie)

menelaos a fost un matematician

grec iar teorema Ce poartă numele

este un instrument util în studiul

coliniaritatea a trei puncte pentru

a demonstra coliniaritatea a 3

puncte se folosește reciproca teoremei

lui menelaus iar pentru aceasta

vom prezenta mai întâi teorema

yacht enunțul acesteia Fie triunghiul

abc și punctele p q r coliniare

este situat pe latura ab q este

situat pe latura AC și n este situat

pe latura a b c Atunci are loc

această relație a p supra pb ori

b r supra RC orice q supra Q A

este egal cu 1 Deci pornim dinți

un vârf al triunghiului de exemplu

din vârful a și avem AB supra pb

ori b r supra RC orice q supra

q a egal cu unu trebuie să ajungem

în același punct din care am plecat

fără să ridicăm creionul de pe

hârtie și fără să trecem de două

ori prin același segment și acum

să vedem cum putem să reținem mai

ușor această relație avem un produs

de 3 rapoarte Iar acest produs

este egal cu 1 fiecare raport începe

cu unul din cele trei vârfuri ale

triunghiului De ce avem A B C primul

raport se termină cu litera cu

care începe următorul raport de

ce aici pe diagonala aceasta copiem

b al doilea raport se termină cu

litera cu care începe următorul

rapport deci pe această diagonală

copiem si ultimul raport se termină

cu litera cu care începe primul

raport de ce avem A acum ne uităm

pe figură pe latura ab a vem punct

ul pe îl copiem și la numărător

și la numitor pe latura bc avem

punctul R îl scriem și sus și în

jos iar pe latura AC a avem punctul

q pe care îl scriem și la numărător

și la numitor Aceasta este o metodă

destul de rapidă de a reține mai

ușor relația din teorema lui menelaus

și acum să vedem Cum demonstrăm

această teoremă vom folosi triunghiurile

asemenea iar pentru aceasta vom

duce prin ce o paralelă la AB care

intersectează dreapta pe r într

un punct pe care îl am notat cu

x așa Dar ce x este paralelă cu

AB se formează două triunghiuri

asemenea triunghiul m b p este

asemenea cu triunghiul a r c x

Haide să le evidențiem mai clar

Iată triunghiul r b p și triunghiul

rcx acestea sunt triunghiuri asemenea

Triunghiul a b p este asemenea

cu triunghiul rcx și avem următoarea

relație de proporționalitate între

laturile acestora iar b supra a

r c este egal cu b p supra c x

mai avem o pereche de triunghiuri

asemenea triunghiul q CX cu triunghiul

q AP acestea sunt unghiuri congruente

pentru că sunt unghiuri opuse la

vârf iar unghiul a p q este congruent

cu unghiul c x q fiind de unghiuri

alterne interne o să notez cu unul

aceste unghiuri Așadar avem aceste

două triunghiuri asemenea triunghiul

q c x este asemenea cu triunghiul

q AP și acum să vedem Cum scriem

rapoartele ne uităm în primul triunghi

latura opusă unghiului 1 este c

q iar în al doilea triunghi latura

opusă unghiului 1 este aq în primul

triunghi latura opusă unghiului

q este CX iar în al doilea triunghi

latura opusă unghiului q este AP

acum înmulțim aceste două relații

membru cu membru din 1 și 2 prin

înmulțire obținem că r b supra

r c ori ce q supra a q este egal

cu b p supra c x ori x supra a

pe aici se simplifică ce x și obținem

RDS supra RC ori cq supra a q egal

cu b supra ape înmulțim toate egalitatea

cu ab supra b p și obținem r b

supra RC ori c q supra acum ori

ab supra b p este egal cu 1 iar

aceasta este chiar în relația din

teorema lui menelaus așadar am

demonstrat această teoremă dreapta

p q r se mai numește transversală

Deci o transversală este o dreaptă

care intersectează cele trei laturi

ale triunghiului dar care nu trece

prin vârfurile acestuia când aplicăm

teorema lui menelaus în rezolvarea

problemelor este bine Indică În

triunghiul pentru care se aplică

teorema și transversală acestuia

să vedem în continuare reciproca

teoremei lui menelaus care se folosește

în demonstrarea coliniaritatea

a 3 puncte Fie triunghiul abc și

punctele p situat pe latura ab

q situat pe latura ac și f situat

pe latura b c astfel încât toate

trei să fie situate pe prelungirile

laturilor triunghiului sau numai

unul pe prelungirea unei laturi

dacă are loc relația a b supra

pe b ori b supra a o c q supra

Q A egal cu 1 atunci punctele p

q și R sunt coliniare în secvența

următoare o să facem o aplicație