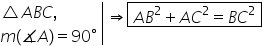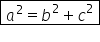Teorema lui Pitagora (aplicații)

în această lecție mă face câteva

aplicații la teorema lui Pitagora

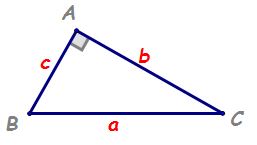
teorema lui Pitagora ne spune că

între un triunghi dreptunghic suma

pătratelor catetelor este egală

cu pătratul ipotenuzei în acest

triunghi dreptunghic catetele sunt

a și b iar ipotenuza este latura

c atunci conform teoremei lui Pitagora

avem următoarea relație a la a

doua plus b la a doua egal cu c

la a doua astfel teorema lui Pitagora

ne ajută să calculăm lungimea ipotenuzei

atunci când se cunosc catetele

unui triunghi dreptunghic este

din această relație putem să exprime

oricare dintre catete în funcție

de ipotenuză și cealaltă catetă

astfel a la a doua va fi egal cu

c la a doua minus b la a doua iar

b la a doua a fi egal cu c la a

doua minus a la a doua rețineți

aceste trei formule pentru că le

vom aplica în exercițiile următoare

începem cu câteva exemple mai simple

avem un triunghi dreptunghic având

catetele cu lungimile de 3 și 4

cm trebuie să aflăm ipotenuza pe

care am notat o cu x din teorema

lui Pitagora obține următoarea

relație 3 la a doua plus 4 la a

doua egal cu x la a doua 3 la a

doua este 9 4 la pătrat este 16

egal cu x la a doua 9 plus 16 este

25 egal cu x pătrat x va fi egal

cu radical din 25 x va fi egal

cu 5 am aflat lungimea ipotenuzei

aceasta este egală cu 5 numerele

3 4 și 5 formează un triplet astfel

de triplete se vor numi triplete

pitagoreice iar tripletul 3 4 5

este unul dintre cele mai des întâlnite

există o infinitate de astfel de

triplete un alt exemplu avem următorul

triunghi dreptunghic atele sunt

egale cu 2 cm și trebuie să aflăm

ipotenuza x Am aplicat din nou

teorema lui Pitagora 2 la a doua

plus 2 la a doua egal cu x la a

doua 4 plus 4 egal cu x la pătrat

8 egal cu x la pătrat x va fi egal

cu radical din 8 putem Să descompunem

numărul 8 iar după ce scoate factorii

de sub radical vom obține 2 radical

din 2 și un al treilea exemplu

se cunoaște o catetă având lungimea

egală cu 6 cm și ipotenuza egală

cu 10 cm trebuie să aflăm Lungimea

celeilalte catete aplicăm din nou

teorema lui Pitagora x la a doua

plus 6 la a doua atenție întotdeauna

se adună catetele egal cu 10 la

a doua am fi putut scrie o altă

relație x la pătrat este egal cu

diferența dintre 10 la pătrat și

6 la pătrat oricare din cele două

relații Este corectă pentru că

se ajunge la același rezultat x

la a doua plus 36 egal cu 100 x

la a doua este egal cu 100 în minus

36 x la a doua este egal cu 64

x va fi egal cu radical din 64

x va fi egal cu 8 continuăm cu

o problemă Se dă un triunghi dreptunghic

ABC cu măsura unghiului a egală

cu 90 de grade m duce înălțimea

AD perpendiculară pe BC Se știe

că ab este egal cu 15 cm ad egal

cu 12 cm trebuie să aflăm lungimea

segmentelor BD bc DC și ac nu scrie

și pe figura a b egal cu 15 și

ad egal cu 12 pentru a afla lungimea

segmentului b d vom aplica teorema

lui Pitagora în triunghiul a d

b deoarece Acesta este un triunghi

dreptunghic a d fiind perpendiculară

pe b c dezvolta că măsura unghiului

adb este egală cu 90 de grade și

atunci va rezulta conform teoremei

lui Pitagora că Ade la pătrat plus

BD la pătrat este egal cu AB la

pătrat 12 la a doua plus b la a

doua este egal cu 15 la a doua

12 la a doua este 144 plus b la

a doua egal cu 225 BD la a doua

este egal cu 225 minus 144 BD la

a doua este egal cu 81 de aici

rezultă că BD este egal cu radical

din 81 și egal cu 9 cm am obținut

bd egal cu 9 cm acum Trebuie să

aflăm lungimea segmentului b c

pentru aceasta putem să aplicăm

teorema catetei În triunghiul abc

din teorema catetei În triunghiul

abc A rezultat că ab la a doua

este egal cu b d ori b c a b este

15 15 la a doua este egal cu 9

ori b c 15 la a doua este 225 egal

cu 9 ori b c împărțim trei realitatea

la 9 și obținem că bc este egal

cu 225 împărțit la 9 a rezultat

de ce este egal cu 25 cm pentru

a afla lungimea segmentului De

ce nu face diferența dintre segmentele

BC și bd De ce este egal cu b c

minus d d egal cu 25 minus 9 egal

cu 16 cm mama și la lungimea segmentului

De ce mai trebuie să aflăm lungimea

segmentului ac AC se poate afla

și Aplicând teorema lui Pitagora

În triunghiul a b c unde se cunoaște

cateta AB și potenza BC și Aplicând

teorema lui Pitagora În triunghiul

abc în acest triunghi se cunosc

cele două catete iar AC este ipotenuza

voi aplica teorema lui Pitagora

În triunghiul adc și acesta este

un unghi drept Așa dat triunghiul

este dreptunghic În triunghiul

abc măsura unghiului ADC este egală

cu 90 de grade și atunci va rezulta

conform teoremei lui Pitagora că

Ade la pătrat plus bc la pătrat

egal cu ace la pătrat a d este

12 iar d c este 16 trebuie să aflăm

latura AC 12 la a doua plus 16

la a doua va fi egal cu ace la

a doua 144 plus 16 la a doua este

256 cu timpul veți învăța și voi

pe de rost pătratele perfecte până

atunci Puteți să faceți calculele

alăturat egal cu AC la pătrat 144

plus 256 este egal cu 400 de g

cu 400 ace va fi egal cu radical

din 400 rezulta ac egal cu 20 cm

am aflat astfel și lungimea laturii

AC aceasta este egală cu 20 cm

continuăm cu o altă problemă problema

numărul 2 Aflați lungimea laturii

unui triunghi echilateral având

înălțimea egală cu 6 radical din

3 avem triunghiul ABC echilateral

ad este înălțime iar lungimea acestuia

este egală cu 6 radical din 3 cm

trebuie să aflăm latura triunghiului

voi nota latura triunghiului cu

litera a dacă ad este înălțime

înseamnă că AD este și mediană

deoarece într un triunghi echilateral

înălțimea coincide cu mediană Așadar

punctul de va fi situat la mijlocul

laturii BC știm că intru în triunghi

echilateral toate laturile sunt

congruente dacă BC are lungimea

egală cu a înseamnă că d c va fi

asupra 2 adică jumătate din lungimea

laturii a teorema lui Pitagora

În triunghiul adc În triunghiul

ABC măsura unghiului adc este egală

cu 90 de grade și atunci mă rezulta

conform teoremei lui Pitagora Ade

la a doua plus b c la a doua este

egal cu AC la a doua AD este 6

radical din 3 plus De ce este asupra

2 totul la a doua egal cu a la

a doua 6 ori 6 este 36 iar radical

din 3 la a doua este 3 plus a la

a doua supra 4 egal cu a la a doua

36 ori 3 este 108 Plus a la a doua

supra 4 egal cu a la a doua trebuie

să separăm termenii care conțin

necunoscuta a de celălalt termen

de numărul 108 ca să rămână în

membrul stâng termenul 108 trebuie

să scădem Termenul care conține

a la a doua supra 4 din ambii membri

obținem astfel că 108 va fi egal

cu a la a doua minus a la a doua

supra 4 pentru a putea efectua

această scădere trebuie să Aduceți

fracțiile la numitor comun amplificăm

prima fracție cu 4 108 egal cu

4-a la a doua supra 4 minus a la

a doua supra 4 108 egal patru a

la a doua minus a la a doua este

3 la a doua supra 4 putem considera

că avem aici O proporție și vom

înmulțit pe diagonală obținem că

3-a pătrat este egal cu 4 ori 108

3a pătrat egal cu 432 astfel aflăm

pe a la a doua împărțit relația

la trei a la a doua egal cu 432

împărțit la 3 la a doua este egal

cu 144 a va fi egal cu radical

din 144 a este egal cu 12 am aflat

astfel latură a triunghiului echilateral

aceasta este egală cu 12