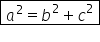Teorema lui Pitagora (teorie)

Tag-uri

Partajeaza in Google Classroom

Partajeaza cu Google Classroom

Susține Lectii-Virtuale!

Pentru a putea vizualiza un video va rugam sa va logati aici! Daca nu aveti cont va puteti inregistra apasand aici.

11 voturi 279 vizionari

Distribuie Raportează eroare

Trimite feedback

Puncte: 10

Transcript

teorema lui Pitagora Pitagora sa

născut pe insula grecească samos

în jurul anului 580 înainte de

Christos a fost filozof și matematice

an există dovezi că această teoremă

era cunoscută cu mult timp înainte

de Nașterea lui Pitagora însă Se

consideră că el a fost primul care

a demonstrat o de aceea sa atribuit

lui vechile popoare indieni babilonienii

și egiptenii antici cunoșteau această

teoremă cu 1.000 de ani înainte

de Nașterea lui Pitagora indiferent

care sunt originile teorema și

consecințele a avut un impact uriaș

asupra omenirii teorema lui Pitagora

se aplică În triunghiul dreptunghic

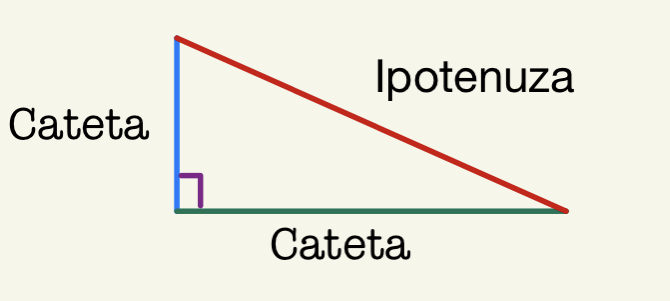
triunghiul dreptunghic este un

triunghi care are un unghi drept

laturile care formează unghiul

drept se numesc catete iar latura

care se opune unghiului drept se

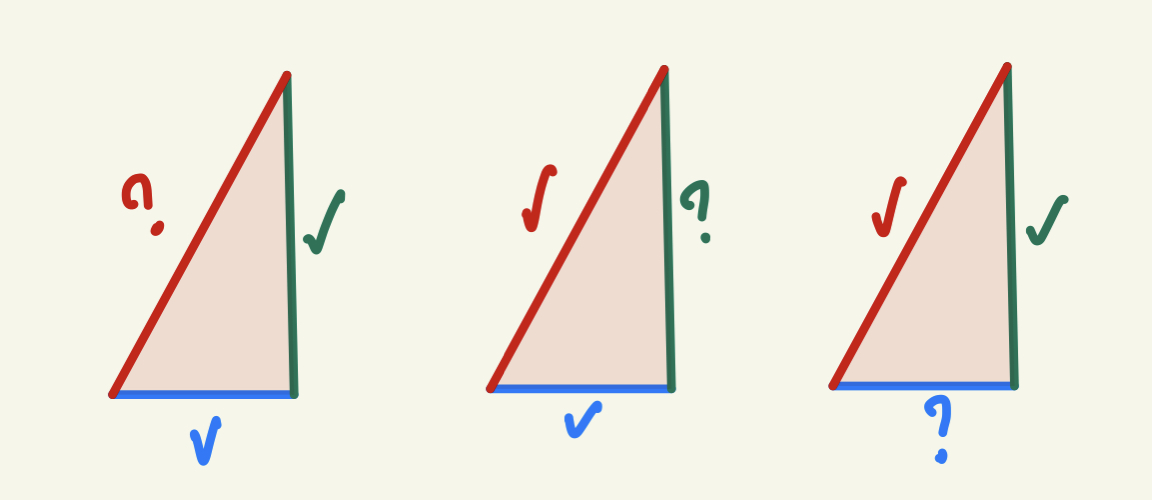
numește ipotenuza trebuie să Recunoașteți

catetele și ipotenuza În orice

triunghi dreptunghic indiferent

de poziția sa sau de notațiile

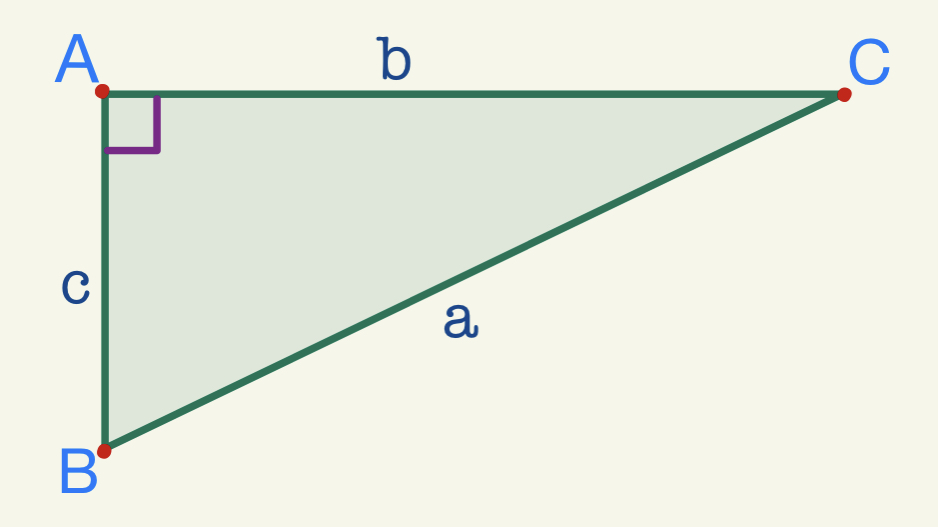
acestuia în a doua figură geometrică

catetele triunghiului sunt a și

b iar ipotenuza este dreapta notată

cu c iar în ultima figura catetele

triunghiului sunt m și n iar ipotenuza

este dreapta notată cu p și acum

să dăm enunțul teoremei lui Pitagora

Într un triunghi dreptunghic suma

pătratelor lungimilor catetelor

este egală cu pătratul lungimii

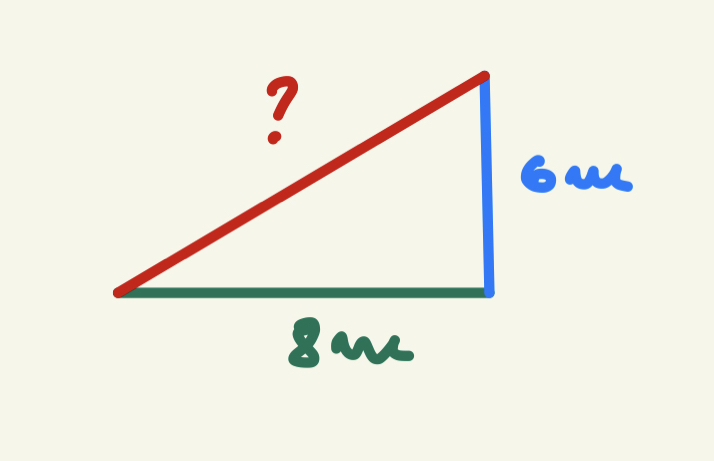
ipotenuzei în acest triunghi dreptunghic

catetele sunt a și b iar ipotenuza

este de 8 Asi astfel conform teoremei

lui Pitagora avem următoarea relație

a pătrat plus b pătrat va fi egal

cu c pătrat această teoremă este

una dintre cele mai importante

teoreme din geometria plană și

ea are peste 300 de demonstrații

o să prezint în continuare două

demonstrații prima demonstrație

avem un triunghi dreptunghic ABC

am dus și înălțimea în acest triunghi

pe care am mutat o cu ad trebuie

să arătăm că ab pătrat plus AC

pătrat este egal cu bc pătrat pentru

această demonstrație voi aplica

de două ori teorema catetei timp

din teorema catetei că a b la pătrat

este egal cu bd ori b c acum aplicăm

teorema catetei pentru cealaltă

catetă a c acela pătrat este egal

cu DC ori b c însumând cele două

relații și obținem că ab pătrat

plus AC pătrat este egal cu bd

ori b c plus d c ori b c observăm

că putem să dăm factor comun b

c și obținem b c pe lângă b d plus

b c dacă ne uităm pe figură b d

plus d c formează lungimea segmentului

b c deci putem scrie egal cu bc

ori b c însă bc ori b c este egal

cu bc la pătrat am demonstrat Așadar

teorema lui Pitagora Folosind teorema

catetei și o să mai fac o demonstrație

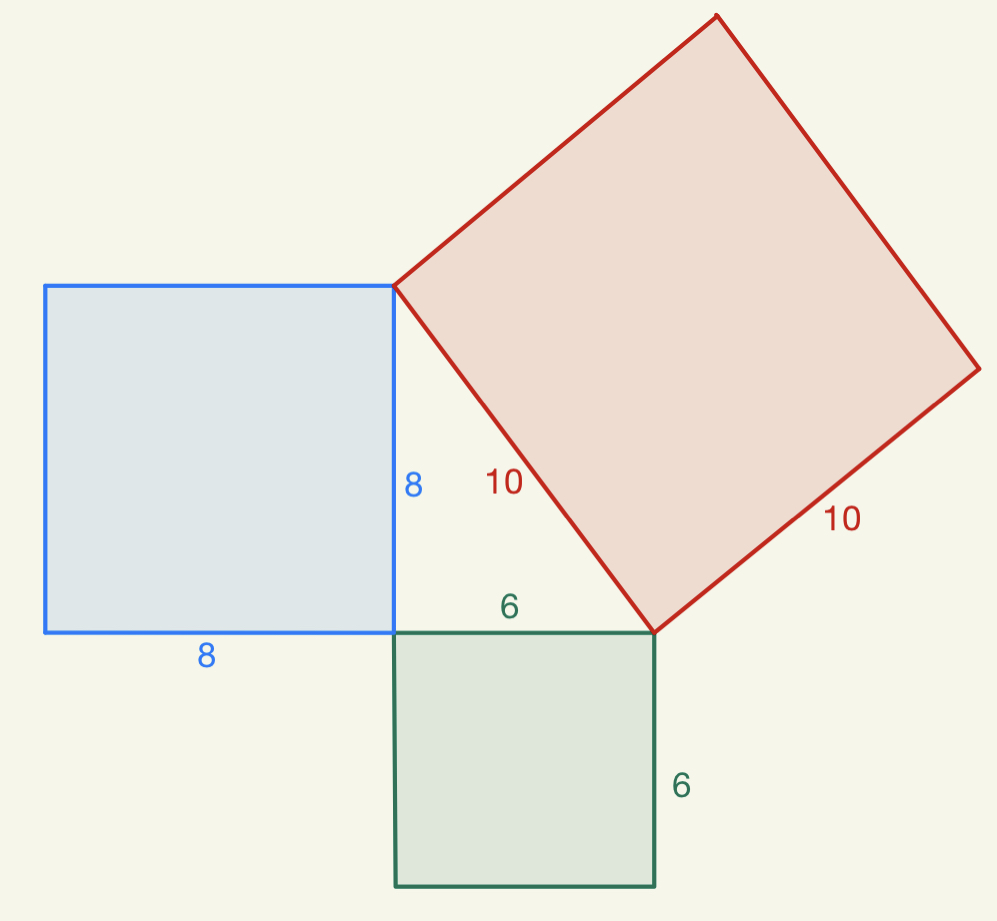
Considerăm că avem un pătrat a

cărui latura sa notat cu litera

C mic este vorba de pătratul alb

din mijloc în exteriorul acestui

pătrat construim patru triunghiuri

dreptunghice congruente catetele

acestor triunghiuri sau notat cu

a și b aria pătratului din centru

este egală cu c la a doua știind

că aria unui pătrat este latura

la puterea a doua latura pătratului

mare este a plus b voi scrie acest

lucru nu latura pătratului din

exterior este a plus b exprima

aria pătratului mare în două moduri

mai întâi aria este latura la a

doua adică a plus b totul la pătrat

dar aria pătratului mare se poate

calcula însumând aria pătratului

alb și cele patru arii ale triunghiurilor

dreptunghice Așadar aria se mai

poate scrie egal cu c pătrat plus

de patru ori aria unui triunghi

dreptunghic dar aria triunghiului

dreptunghic este produsul catetelor

supra 2 catetele acestor triunghiuri

sunt a și b Deci voi Scrie patru

ori ab supra 2 egal se simplifică

4 și 2 și obținem c pătrat plus

2 a b egalăm cele două arii și

obține următoarea relație a plus

b totul la pătrat egal cu c pătrat

plus 2ab pentru a calcula pătratul

acestei sume folosind formule de

calcul prescurtat învățate la algebră

astfel a plus b totul la a doua

este egal cu a doua plus doi a

b plus b la a doua egal în continuare

cu ce pătrat plus 2ab termenul

2ab se reduce pentru că are același

semn și este situat în membrii

diferiți și obținem că a pătrat

plus b pătrat este egal cu c pătrat

ținând cont de faptul că a b și

c erau Laturile unui triunghi dreptunghic

rezultatele ma lui Pitagora este

demonstrată observăm astfel că

teorema lui Pitagora Realizează

o legătură interesantă între geometrie

și algebră să vedem în continuare

unde vom aplica această teoremă

teorema lui Pitagora se poate aplica

în cazul în care dorim să calculăm

înălțimea în triunghi isoscel sau

atunci când ne propunem să calculăm

Latura unui romb atunci când se

Cunoscând diagonalele sale în clasa

a opta o să aplicăm teorema lui

Pitagora atunci când vom calcula

diferite elemente ale unei piramide

cum ar fi înălțimea sau apotema

B5 pten au folosit teorema lui

Pitagora atunci când a fost Street

piramidele din Egipt teorema lui

Pitagora a făcut posibilă apariția

unei ramuri importante a matematicii

numită trigonometrie aceasta se

ocupă cu studiul relațiilor dintre

laturile și unghiurile unui triunghi

multe dintre triunghiurile din

viața reală nu sunt dreptunghice

însă orice triunghi poate fi împărțit

în două triunghiuri dreptunghice

și 8 c forma poligonală poate fi

împărțită în triunghiuri astfel

triunghiul dreptunghic este fundamental

în trigonometrie aplicarea teoremei

lui Pitagora Este posibilă și în

cazul triunghiurilor oarecare prin

folosirea formei generalizate a

acesteia în liceul veți învăța

și teorema lui Pitagora generalizată

pentru triunghiuri oarecare teorema

lui Pitagora a dezvăluit forma

planetei noastre și locul ei în

univers Ea a fost un pas Vital

către tehnicile geometrice necesare

pentru cartografiere navigație

și topografie având la dispoziție

ecuații trigonometrice și instrumente

adecvate de măsură a fost posibilă

realizarea hărților precise sa

dezvoltat Astăzi topografia adică

știința care se ocupă cu tehnica

măsurătorilor unei porțiuni de

teren în scopul întocmirii hărților

în anul 1615 un matematician olandez

a folosit pentru întocmirea unei

hărți un procedeu numit triangulație

suprafața topograf Iată era acoperită

cu o rețea de triunghiuri și cu

ajutorul ecuațiilor trigonometrice

a fost posibilă calcularea unor

distanțe și unghiuri acest matematician

și taie astfel să calculeze mărimea

pământului triangulația a făcut

posibilă și calcularea înălțimii

muntelui Everest în secolul nostru

întocmirea hărților se realizează

folosind o se fotografii din satelit

și sistemul de poziționare în globală

așa numitul GPS nu se mai folosește

triangulația explicită însă ia

continuă să existe în Metodele

folosite pentru aflarea localizări

lor din datele primite de la satelit

Pitagora la inspirat și pe Einstein

acesta folosind geometria triunghiului

în teoria generală a relativității

extinderea teoremei la triunghiului

oarecare nea permisă cartografie

în continentele și să ne măsurăm

planeta astfel teorema lui Pitagora

nu ne ajută doar să calculăm diagonala

unui televizor ea ne permite să

măsurăm forma universului

Teorema lui PitagoraAscunde teorie X

Teorema lui Pitagora - ce trebuie să știi

Istoric

Ce este o teoremă

Enunțul teoremei lui Pitagora

Un exemplu practic

Reprezentarea geometrică a teoremei lui Pitagora

La școală

Vezi și

Istoric

Teorema lui Pitagora este una dintre cele mai cunoscute teoreme din Matematică. Teorema este atribuită lui Pitagora, un matematician din Grecia Antică (c. 570 – c. 495 î.Hr.) deși există unele izvoare istorice care sugerează că aceste lucruri erau cunoscute dinainte de Pitagora. Teorema lui Pitagora este foarte importantă pentru omenire. În timpuri străvechi, teorema lui Pitagora le-a permis strămoșilor noștri să navigheze. Ulterior, pe baza teoremei lui Pitagora oamenii de știință au făcut descoperiri importante în domenii precum cartografia (= știința de a face hărți) și trigonometria (= ramură a matematicii care studiază relația dintre laturile și unghiurile unui triunghi).

Ce este o teoremă

Este posibil să nu fi auzit cuvântul teoremă foarte des înainte de a învăța despre teorema lui Pitagora. Înainte să discutăm despre teorema lui Pitagora e bine să știm în general ce este o teoremă. O explicație pe înțelesul tuturor este că o teoremă este o afirmație cu conținut matematic. Dar asta nu e tot. Afirmația conținută în teoremă s-a demonstrat prin mijloace matematice că este adevărată. Teoremele sunt importante pentru că ne ajută să înțelegem lucruri noi și să rezolvăm probleme. De aceea trebuie să le înțelegem și să le memorăm.

Enunțul teoremei lui Pitagora

Teorema lui Pitagora stabilește o relație între cele trei laturi ale unui triunghi dreptunghic și sună în felul următor: într-un triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei. Dacă nu știți ce este o catetă și ce este o ipotenuza explicăm pe scurt. Un triunghi dreptunghic conține un unghi de 90 de grade. Cele două laturi alăturate unghiului de 90 de grade se numesc catete în timp ce latura opusă unghiului de 90 de grade se numește ipotenuză.

În mod frecvent, catetele și ipotenuza se notează cu litere mici ca în exemplul de mai jos.

Acest exemplu ne permite să scriem următoarea concluzie:

$\newline \bigtriangleup ABC, m(\measuredangle A) = 90\degree \newline \newline => AB^2 + AC^2=BC^2 \newline \newline sau \newline \newline \bigtriangleup ABC, m(\measuredangle A) = 90\degree \newline \newline => b^2+c^2=a^2$

Pe scurt:

$box enclose space a squared equals b squared plus c squared space end enclose$

Un exemplu practic

Să presupunem că avem o casă ca în desenul de mai jos și că vrem să tragem un fir electric de la priza din stânga la priza din dreapta imaginii. Deși nu am desenat ne putem închipui că avem pereți interiori și mobilă care nu ne permit să măsurăm direct lungimea acestui fir. Cum altfel am putea face? Evident, putem afla lungimea firului nostru cu ajutorul teoremei lui Pitagora.

Observăm că muchia casei reprezentată cu albastru are 6 metri și cea reprezentată cu verde are 8 metri și că unghiul format de cele două muchii figurat cu violet este de 90 de grade. Firul nostru va fi reprezentat de segmentul de culoare roșie care reprezintă în același timp ipotenuza. Am reprezentat mai jos aceeași podeau casei și trinunghiul dreptunghic format de cele trei segmente.

Notăm lungimea firului nostru cu x și aplicând teorema lui Pitagora obținem că:

$\newline \newline 8^2 + 6^2=x^2 \newline 64 + 36= x^2 \newline 100 =x^2\newline => x =\sqrt{100} \newline => x = 10$

Prin urmare, lungimea firului nostru este de 10 metri. Nu trebuie să uităm unitatea de măsura. De asemenea, nu uitați că lungimile segmentelor în teorema lui Pitagora sunt la puterea a doua sau la pătrat. Ca să afli de ce lungimile segmentelor din teorema lui Pitagora sunt la puterea a doua și care este legătura cu figura geometrică reprezentată de pătrat citește mai jos.

Reprezentarea geometrică a teoremei lui Pitagora

Se pare că atunci când Pitagora încerca să găsească o demonstrație pentru observațiile sale despre laturile triunghiului dreptunghic, el a văzut o legătură între ariile pătratelor care se pot construi pe baza laturilor unui triunghi dreptunghic. În figura de mai jos am reprezentat la scară aceleași dimensiuni ale triunghiului din problema de mai sus (6 și 8 metri pentru catete și respectiv 10 metri pentru ipotenuză) dar de data aceasta am reprezentat și cele trei pătrate care se pot construi plecând de la acest triunghi dreptunghic.

Stim că un pătrat este o figură geometrică, mai bine zis un poligon, în care toate laturile sunt egale (= congruente) și paralele două câte două. Aria unui pătrat se obține înmulțind două laturi între ele sau altfel sus, ridicând lungimea unei laturi la puterea a doua. Spre exemplu, în figura de mai sus:
Pătratul verde are aria de $6 cm * 6 cm = 36 cm ^2$
Pătratul albastru are aria de $8 cm * 8 cm = 64 cm^2$
Pătratul roșu are aria de $10 cm * 10 cm = 100 cm^2$
Observați: Pătratul verde + Pătratul albastru = Pătratul roșu (36cm² + 64cm²=100cm²) sau cu alte cuvinte, suma pătratelor formate de catete este egală cu pătratul format pe baza ipotenuzei.

O altă idee interesantă este că unui segment putem să-i măsurăm lungimea dar un segment considerat de unul singur are o singură dimensiune - lungimea sa. Lungimea unui segment se poate măsura ca fiind 1 milimetru (1 mm), 1 centimetru (1cm), 1 metru ș.a.m.d. Ei bine, spre deosebire de lungimea unui segment care este unidimensională, aria unui pătrat este bidimensională. Adică aria unui pătrat se obține prin înmulțirea a două laturi și de aceea unitate de măsură a ariei este la puterea a doua (1 mm², 1 cm², 1 m² ș.a.m.d) sau se mai spune și la pătrat.

La școală
În general, la școală vi se vor da probleme în care fie se cunoaște lungimea catetelor și se cere să se calculeze lungimea ipotenuzei, fie se cunoaște lungimea unei catete și a ipotenuzei și se cere să se calculeze lungimea celeilalte catete. Vă invităm să faceți înlocuirile în figura de mai jos și să vedeți dacă obțineți rezultatele corecte. În primul triunghi se cere calcularea ipotenuzei - deja am rezolvat mai sus pe pagină acest caz. Vă invităm să faceți înlocuirile în celelalte două exemple și să vedeți dacă puteți calcula corect lungimea catetei mari (cu verde) și a catetei mici (cu albastru).

Vezi și
Teorema lui Pitagora - lecție video
Teorema lui Pitagora - exerciții rezolvate

Vezi mai mult...

Navigare în lectii

Cumpara abonament

Plătește cu PayPal

Ajutor

Feedback-ul d-voastră este important pentru noi. Dacă observați vreo neregulă vă rugăm să ne-o semnalați apăsând butonul Trimite Feedback de mai jos.

Cumpara abonament!

Teorema lui Pitagora (teorie)

Tag-uri

Partajeaza in Google Classroom

Transcript

Teorema lui PitagoraAscunde teorie X

Teorema lui Pitagora - ce trebuie să știi

Istoric

Ce este o teoremă

Enunțul teoremei lui Pitagora

Un exemplu practic

Reprezentarea geometrică a teoremei lui Pitagora

La școală

Vezi și

Navigare în lectii

Cumpara abonament

Ajutor

Despre Lecții-Virtuale.ro

Newsletter

Parteneri

Clase

Discipline

Evaluare Nationala

Bacalaureat

Clase

Discipline

Evaluare Nationala

Bacalaureat

Clase

Discipline

Evaluare Nationala

Bacalaureat

Clase

Discipline

Evaluare Nationala

Bacalaureat

CCD Galați

Bun Pi Mate

Mate cu Lavinia

Cumpara abonament!

Teorema lui Pitagora (teorie)

Tag-uri

Partajeaza in Google Classroom

Transcript

Teorema lui PitagoraAscunde teorie X

Teorema lui Pitagora - ce trebuie să știi

Istoric

Ce este o teoremă

Enunțul teoremei lui Pitagora

Un exemplu practic

Reprezentarea geometrică a teoremei lui Pitagora

La școală

Vezi și

Navigare în lectii

Cumpara abonament

Ajutor

Despre Lecții-Virtuale.ro

Newsletter

Parteneri