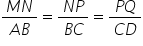Teorema paralelelor neechidistante

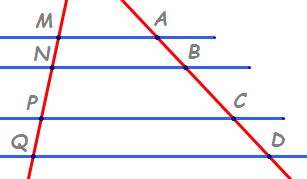
teorema paralelelor neechidistante

trei sau mai multe drepte paralele

determină pe două secante segmente

proporționale avem patru drepte

paralele notate cu D1 D2 D3 și

D4 și două secante a și b secanta

a intersectează cele patru drepte

paralele în punctele a b c și d

iar secanta a b intersectează dreptele

în punctele a prim b prim c prim

și D prim atunci are loc următoarea

relație a b supra a prim b prim

va fi egal cu b c supra b prim

c prim și egal cu cd supra c prim

D prim această teoremă se poate

aplica atunci când dorim să împărțim

un segment împărțit raport ționale

cu anumite numere date nu face

această aplicație Fie AB un segment

cu lungimea de 9 cm Împărțiți segmentul

în patru părți proporționale cu

numerele 2 3 4 și 5 mai întâi vom

duce prin punctul a O dreaptă pe

care o notăm cu a m și pe această

dreaptă fixăm punctele c d și e

astfel încât segmentul AC să fie

egal cu 2 cm segmentul CD să aibă

lungimea de 3 cm segmentul d e

are lungimea de 4 cm iar segmentul

m să fie cu lungimea de 5 cm pentru

a Împărțiți segmentul ab în părți

proporționale cu aceste numere

m mai întâi punctele m și b apoi

prin celelalte puncte c d e paralel

A la dreapta b m iar punctele în

care aceste drepte paralele intersectează

segmentul ab le vom nota cu e f

g și h astfel am reușit să împărțim

din punct de vedere geometric segmentul

ab în patru părți proporționale

cu numerele 2 3 4 și 5 și acum

putem calcula în continuare lungimea

segmentelor a f f g g h și h d

din teorema paralelelor neechidistante

deducem următoarea relație a f

supra ac este egal cu fg supra

CD egal cu g h supra d e f și egal

cu HB supra i m segmentele a c

c d d e și e m au lungimile de

2 3 4 și respectiv 5 cm a f supra

2 egal cu f g supra 3 egal cu gh

supra 4 și egal cu h b supra 5

dar folosind proporții derivate

aceste rapoarte se pot egala mai

departe cu raportul format de suma

numărătorilor și suma numitorilor

Deci avem a f plus f g plus g h

plus HB supra 2 plus 3 plus 4 plus

5 dar a f plus f plus g h plus

h b formează lungimea segmentului

AB iar aceasta este egală cu 9 cm

iar 2 plus 3 este 5 plus 4 9 plus

5 14 făcând separat această împărțire

9 la 14 se obține 0 iar acum ca să

aflăm aceste segmente egalăm fiecare

raport cu rezultatul obținut a

e supra 2 este egal cu 0 is va fi

egal cu 2 ori 0 egal cu 1 cm f g

supra 3 este egal cu 0 rezultă că

e f g este egal cu 3 ori 0 egal

cu 2 cm gh supra 4 egal cu 0 rezultă

c h egal cu patru ori 0 și egal

cu 2 cm Haș b supra 5 egal cu 0 h

b egal cu 5 ori 0 egal cu 3 cm am

reușit astfel Să împărțim un segment

având o lungime dată în părți proporționale

cu numerele 2 3 4 și 5 Folosind

teorema paralelelor neechidistante