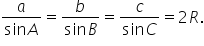Teorema sinusurilor (teorie)

ca și teorema cosinusului teorema

sinusurilor exprimă o relație între

laturile și unghiurile unui triunghi

oarecare dar în această teoremă

intervine și noțiunea de raza cercului

circumscris orice triunghi are

un cerc circumscris iar centrul

acestui cerc este la intersecția

mediatoarelor pentru cei care nu

știu O mediatoare este o perpendiculară

dusă prin mijlocul unui segment

În triunghiul abc mediatoarele

laturilor triunghiului sunt aceste

segmente desenate punctat cu roz

mediatoarele se intersectează în

punctul O iar o este centrul cercului

circumscris triunghiului mo tot

laturile triunghiului abc cu a

mic b mic și c mic am construit

și diametrul BM prin urmare segmentele

b o și o m sunt raze ale cercului

circumscris triunghiului și acum

să vedem relația din teorema sinusurilor

a supra sinus de aer sta egal cu

b supra sinus de b egal cu c supra

sinus de c și egal cu 2 r Deci

in orice triunghi raportul dintre

o latură și sinusul unghiului opus

este egal cu diametrul cercului

circumscris triunghiului vom demonstra

această teoremă în cazul în care

triunghiul este ascuțitunghic dreptunghic

și respectiv obtuzunghic mai întâi

studiem cazul din imagine în care

triunghiul este ascuțitunghic o

să unim punctele m cu c și astfel

sa format triunghiul b m c dreptunghic

în c având în vedere că BM este

diametru unghiul c este un unghi

drept să scriem demonstrație În

triunghiul b m c unghiul c are

măsura egală cu pi supra 2 radiani

să exprimăm din acest triunghi

sinus de m sau sinus de b m c sinusul

acestui unghi este raportul dintre

cateta opusă unghiului m adică

BC supra ipotenuza b m b c este

a mic iar b m este 2 r observăm

că unghiul bac este congruent cu

unghiul BMC deoarece laturile acestuia

două unghiuri sub întind același

arc b c prin urmare unghiul bac

este congruent cu unghiul BMC din

aceste două relații rezultă că

sinus de BAC va fi egal cu a supra

2 r Ia de aici obținem relația

a supra sinusul unghiului BAC sau

mai simplu sinus de a este egal

cu 2 r în mod asemănător se demonstrează

și celelalte două relații b supra

sinus de B este egal cu c supra

sinus de c și egal cu 2 trecem

în continuare la cazul al doilea

în care triunghiul ABC este dreptunghic

în A avem în imagine triunghiul

ABC cu măsura unghiului a egală

cu pi supra 2 Radian trebuie să

demonstrăm următoarea relație a

supra sinus de ei dar sinus de

pi supra 2 este 1 egal cu b supra

sinus de b egal cu c supra sinus

de ce și egal cu 2 r însă având

în vedere că triunghiul b a c este

dreptunghic în A A potenza BC este

egală cu diametrul cercului circumscris

triunghiului prin urmare a este

egal cu 2 r aceasta este relația

pe care trebuie să o demonstrăm

în continuare din triunghiul bac

exprimăm sinus de b și avem sinus

de b egal cateta opusă b mic supra

ipotenuza a mic prin urmare b supra

sinus de b egal cu a mic apoi sinus

de c este egal cu c supra a c supra

sinus de c este egal cu a mic am

demonstrat această relație și trecem

la cazul următor în care triunghiul

ABC este obtuzunghic avem triunghiul

ABC obtuzunghic Deci măsura unghiului

a este mai mare de 90 de grade

și am construit diametrul bem o

să unim punctele m cu c și astfel

se format patrulaterul a b m c

Acesta este un patrulater inscriptibil

în consecință unghiurile opuse

sunt suplementare deci a plus m

este egal cu pi triunghiul bcm

este dreptunghic în C un dulce

este drept pentru că BM este diametru

și atunci să exprimăm din acest

triunghi sinus de m sinus de m

este egal cu raportul dintre cateta

opusă unghiului m adică BC supra

ipotenuza de m și egal în continuare

cu a supra 2 iar m este pe minus

a prin urmare sinus de pi minus

a este egal cu a supra 2 r dar

sinus de pi minus a este egal cu

sinus de a am văzut acest lucru

în lecția în care am discutat despre

reducerea la primul cadran și atunci

sinus de am dar fie egal cu a supra

2 r și în final obținem relația

a supra sinus de a este egal cu

2 r în mod asemănător se demonstrează

și celelalte două relații b supra

sinus de B este 2 r și c supra

sinus de c este 2 r în secvența

următoare o să facem câteva aplicații