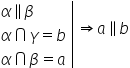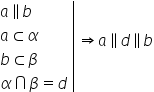Teoreme de paralelism
Tag-uri
Partajeaza in Google Classroom

Transcript
în această secvență vrem să prezentăm
câteva teoreme de paralelism pe
care e foarte bine să le reținem
pentru că le vom folosi apoi în
probleme Ce înțelegem prin plane
paralele două plane sunt paralele
dacă nu au niciun punct în comun
Alfa intersectat cu b ca este mulțimea
vidă Cum arătăm însă că două plane
sunt paralele avem următoarea teoremă
dacă un plan conține două drepte
concurente paralele cu un alt plan
Atunci cele două plane sunt paralele
Deci dacă între un plan alfa Avem
două drepte a și b deci a și b
sunt inclusă în planul alfa iar
aceste două drepte sunt concurente
a intersectat cu b avem aici punctul
a d sunt concurente în acest punct
și Dacă dreptele a și b sunt paralele
cu un alt plan Deci Dacă dreapta
a mic este paralelă cu planul Beta
și dreapta b mic este paralel și
a la rândul ei cu planul Beta atunci
conform acestei teoreme Ce rezultă
că cele două plane sunt paralele
Alfa paralel cu Beta Deci ca Să
arătăm că două plane sunt paralele
trebuie să arătăm că între un plan
există două drepte concurente care
sunt paralele cu celălalt plan
și atunci cele două plane sunt
paralele și o altă teoremă această
teoremă nu ne spune cum Să arătăm
că două plane sunt paralele Dar
ne spune următorul lucru Dacă o
dreaptă este paralelă cu un plan
alfa și dreapta este inclusă în
plan Beta Beta second cu alfa atunci
dreapta a este paralela cu dreapta
intersecția planelor Alfa și Beta
bun să reluăm dacă o dreaptă a
adică dreapta a este paralela cu
un plan alfa iar Aici planul alfa
ești nici notăm a paralelă cu alfa
și dreapta a este inclusă în plan
Betta dreapta a este inclusă în
acest plan Betta a inclusă în Deta
acest plan Beta este second cu
alfa Deci Alfa și Beta sunt plane
secante Ce înseamnă asta Că intersecția
lor este o dreaptă Haide so trasăm
trecem aici dreapta de dreapta
de intersecție a planelor Alfa
și Beta bun atunci dreapta a adică
aceasta este paralelă cu dreapta
de intersecție a planelor Alfa
și Beta Deci din aceste relații
conform aceste teoremei rezultă
că dreapta a este paralela cu dreapta
d a paralelă cu d o altă teoremă
se numește teorema fierăstrăului
care ne spune că Dacă două plane
paralele sunt intersectate de un
al treilea plan atunci dreptele
de intersecție sunt paralele prin
urmare Dacă două plane paralele
Alfa și Beta sunt plane paralele
Alfa paralel cu Beta dacă ele sunt
intersectate de un al treilea plan
planul gama Iată intersectează
fiecare din cele două plane planul
gama intersectat cu planul alfa
să trecem aici că avem dreapta
c mic și o și Reprezentăm iar planul
gama intersectat cu planul Beta
și să trecem că avem dreapta d
mic și o Reprezentăm și pe desen
de ce aici avem dreapta c mic și
aici dreapta d mic atunci conform
acestei teoremei ce se spune că
dreptele de intersecție adică dreptele
c și d sunt drepte paralele se
vede acest lucru și pe desen Deci
venim aici și trecem rezultă că
dreapta c este paralelă cu dreapta
numele este destul de sugestiv
pentru că dacă ne imaginăm că planul
gama este un fierăstrău atunci
putem să citim că Dacă două plane
paralele Alfa și Beta sunt tăiate
de un al treilea plan gama Tae
cele două plane atunci dreptele
de intersecție c și d sunt paralele
teoremă foarte ușor de reținut
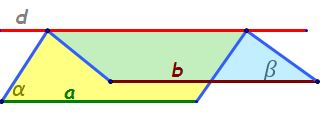
următoarea teoremă are și ea un
nume și se numește teorema acoperiș
observăm că și figura arată ca
un acoperiș de ceata de unde și
numele și ne spune că dacă dreptele
paralele a și b sunt inclusă în
planele secante Alfa și Beta atunci
dreptele a și b sunt paralele cu
dreapta de intersecție a celor
două plane Prin urmare avem două
drepte paralele a și b dreapta
Paralelă cu dreapta b dreapta a
este paralela cu dreapta b și știind
că dreptele a și b sunt inclusă
în planele secante Alfa și Beta
planul alfa și planul Beta sunt
plane secante Alfa intersectat
cu b taie dreapta de intersecție
este nota tăiată de mic și știind
că dreapta a mic este inclusă în
planul alfa Deci am inclusă în
Alfa și dreapta b mic este inclusă
în planul Beta să trecem aici dreapta
b inclusă în Beta atunci dacă tu
aceste condiții sunt îndeplinite
dreptele a și b sunt paralele și
dreptele a și b sunt paralele cu
dreapta de intersecție a celor
două plane adică cu dreapta d rezultă
din această teoremă că dreapta
a este paralela cu dreapta d paralelă
la rândul ei cu dreapta b mic altă
teoremă este teorema lui Thales
în spațiu care ne spune că mai
multe plane paralele determină
pe două secante segmente proporționale
Deci dacă avem planul alfa paralel
cu Beta și la rândul său paralel
și cu gama Deci planele Alfa Beta
și Gamma sunt plane paralele și
avem dreptele a c și a prim c prim
sau putem să le denumim AB și a
prim D prim ca în figură atunci
vom avea segmente proporționale
cu alte cuvinte a b segmentul ab
lungimea segmentului AB supra lungimea
segmentului a prim D prim este
egală cu lungimea segmentului BC
supra lungimea segmentului b prim
c prim și ultima teoremă Care este
foarte simplă teorema de tranzitivitate
a relației de paralelism două plane
paralele cu un al treilea plan
disting de primele două sunt paralele
între ele Deci dacă planul alfa
este paralel cu planul Beta și
planul Beta la rândul său este
paralel cu planul gama atunci rezultă
că planele Alfa și Gamma sunt paralele
planele Alfa și Gamma sunt plane
paralele Toate aceste teoreme sunt
câteva dintre teoremele de paralelism
și eu zic că sunt destul de importante
pentru că le vom aplica și în probleme

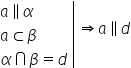
.JPG)