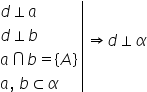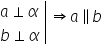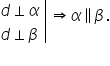Teoreme de perpendicularitate

în continuare enumerăm câteva teoreme

importante de perpendicularitate

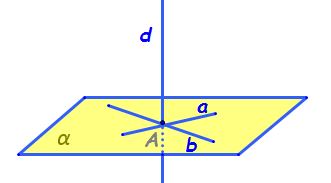
pe prima deja o cunoaștem O dreaptă

este perpendiculară pe un plan

dacă este perpendiculară pe două

drepte concurente din acel plan

Deci dreapta d este perpendiculară

pe dreapta a mic dreapta d perpendiculară

pe a mic atenție să nu ne sperie

aici faptul că nu am mai desenat

dreapta d perpendiculară pe dreptele

a și b în punctul A și am desenat

o aici și nu concurentă cu cele

două drepte chiar și așa dreptele

d și a sunt drepte necoplanare

dar unghiul format de ele este

tot de 90 de grade deci putem să

scriem că dreptele d și a dreptei

perpendiculare la fel dreapta d

perpendiculară pe dreapta b dreptele

a și b sunt drepte concurente se

intersectează în p pula mare ele

fac parte din planul alfa sunt

incluse în Alfa atunci din toate

aceste relații și din teorema de

mai sus rezultă că dreapta d este

perpendiculară pe plan de trecem

D perpendiculară pe alfa o altă

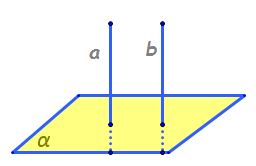
teoremă două drepte perpendiculare

pe un același plan sunt paralele

Deci dacă avem dreptele a și b

perpendiculare pe un plan a perpendiculară

pe planul alfa iar dreapta b este

perpendiculară tot pe planul alfa

atunci rezultă că dreptele a și

b sunt drepte paralele a paralelă

cu b și o altă teoremă dacă o dreaptă

este perpendiculară pe două plane

Atunci cele două plane sunt paralele

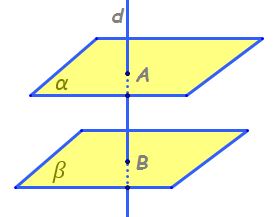
în această situație avem dreapta

d perpendiculară și pe planul alfa

Pe planul gama Deci dreapta d perpendiculară

pe Alfa dreapta d este perpendiculară

în același timp și pe gama atunci

rezultă că cele două plane sunt

paralele Alfa paralel cu gama Deci

când avem o dreaptă perpendiculară

pe două plane înseamnă că cele

două plane sunt paralele nu vom

face demonstrațiile acestor de

aur ma însă e foarte bine să le

reținem pentru că le vom folosi

în probleme