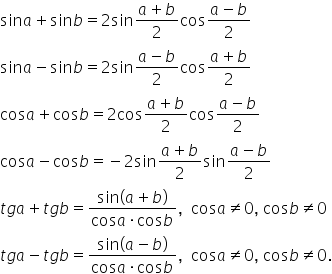Transformarea sumelor în produse

pentru a aduce unele expresii la

o formă mai simplă trebuie să transformăm

sumele de funcții trigonometrice

în produse în acest clip ne propunem

se găsi formulele pentru sinus

de a plus sinus de B sinus de a

minus sinus de B cosinus de a plus

cosinus de b respectiv cosinus

de a minus consiliul de B pentru

aceasta Avon pornind de la aceste

două formule sinusul sumei respectiv

sinusul diferenței mă faci următoarea

substituție o să notez x plus y

cu a și x minus y cu b adunând

aceste două relații obținem 2 x

egal cu a plus b de unde x este

egal cu a plus b supra 2 iar scăzând

cele două relații obținem 2 y egal

cu a minus b iar y este egal cu

a minus b pe 2 Revenim la aceste

două formule și adunând relațiile

1 și 2 vom obține sinus de a plus

sinus de b egal țin de x poți de

y și avem 2 sinus de y pornim de

la formula pentru cosinus sumei

respectiv Consiliul diferenței

adunând relațiile 1 și 2 vom avea

a cosinus de a plus cosinus de

b egal termenul cu sin de x si

y se reduce și obținem 2 cozi de

x coș de x unde x este a plus b

supra 2 iar y este a minus b supra

2 scăzând relațiile 1 și 2 avem

cozi de a minus coș de B anal se

reduce termenul cozi de x cos de

y și vom avea minus 2 sinus de

x sinus de x y unde x este A plus

B pe 2 iar y este a minus b supra

2 am demonstrat Așadar alte două

formule de transformare a sumelor

în produse Și mai trebuie să investim

și formulele pentru tangentă ne

propunem să găsim formula pentru

tangentă de a plus tangentă de

B mai exact dorință transformăm

această sumă între un produs știind

că tangenta este raportul dintre

sinus și cosinus de C tangentă

de a este sinus de asupra cosinus

de a iar tangentă de B este sinus

de b supra cosinus de B aducem

la numitor comun și obținem sinus

de a cosinus de b plus caz de a

sinus de B totul supra cosinus

de a ori cosinus de B dar țin de

acord de b plus cos de a sinus

de B este sinus de a plus b supra

cos de a b să reținem Așadar formula

tangentă de a plus tangentă de

b egal cu sinus de a plus b supra

cosinus de a cosinus de B în mod

asemănător se demonstrează formula

tangentei de a minus tangentă de

b egal cu sinus de a minus b supra

cosinus de a cosinus de B aceste

rapoarte există dacă numerele cosinus

de a și cosinus de B sunt diferite

de 0