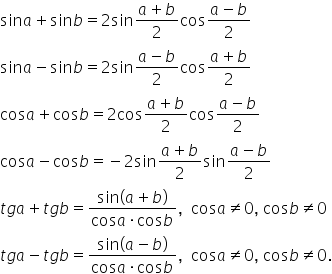Transformarea sumelor în produse (aplicații)

în acest clip vă rezolvat câteva

exerciții în care voi aplica formulele

de transformare a sumelor in produs

în prima exercițiu se cere să transformăm

în produs cosinus de 75 de grade

minus cosinus de 15 grade aplicăm

ultima formulăm și vom avea minus

2 sinus de 75 plus 15 grade supra

2 ori sinus de 75 minus 15 grade

supra 2 egal cu minus 2 sinus 75

plus 15 este 90 pe 2 45 de grade

ori sinus de 75 minus 1560 pe 230

inel cu minus 2 ori radical din

2 pe 2 ori 1 pe 2 egal cu minus

radical din 2 pe 2 următorul exercițiu

se cere să transformăm în produs

sinus de pi supra 8 plus sinus

de 5.000 supra opt aplicăm prima

formulăm și avem 2 sinus dep supra

8 plus 5 supra 8 totul pe 2 ori

cosinus de pi supra 8 minus 5 supra

8 totul supra 2 egal cu 2 sinus

aici obținem 6 pipe 8 se simplifică

și ne dă 3 pe 4 totul supra 2 adică

trei pipe 8 ori cosinus pipi 8

minus 5 pe 8 este minus 4 pai pe

8 se simplifică și ne dă minus

pi supra 2 totul supra 2 este minus

pi pe 4 egal funcția cosinus este

o funcție pară Deci cosinus de

minus y supra 4 este egal cu cosinus

de pi pe 4 avem Așadar 2 sinus

de 3pi pe opt ori cosinus de pi

supra 4 cosinus de pi pe 4 este

radical din 2 pe 2 iar finul de

3 pi supra 8 Rămâne așa iar rezultatul

final vei fi radical din 2 ori

sinus de 3pi supra 8 următorul

exercițiu avem următoarea fracție

cosinus de 20 de grade plus sinus

de 20 de grade supra cosinus de

20 minus sinus de 20 se cere să

simplificăm această fracție observăm

că nu avem o formulă pentru suma

dintre sinus și cosinus din acest

motiv ne propunem să exprimăm cosinus

de 20 în funcție de sinus amintesc

formula unghiurilor complementare

cosinus de x este egal cu sinus

de pi pe 2 minus x prin urmare

cosinus de 20 de grade va fi egal

cu sinus de 90 de grade minus 20

Deci cosinus de 20 de grade este

egal cu sinus de 70 și acum să

revenim la exercițiu Deci în loc

de cosinus de 20 V scrie sinus

de 70 avem sinus de 70 de grade

plus sinus de 20 supra sinus de

70 minus sinus de 20 de L la numărător

aplicăm formula sinus de a plus

sinus de b și Avem doi ori sinus

de A plus B pe doi adică 70 plus

20 90 supra 245 ori cosinus de

70 minus 2050 pe 225 supra țin

de a minus sin de B este 2 sinus

de a minus b pe doi Deci avem doi

ori sinus de 70 minus 20 pe 2 25

ori cosinus de 70 plus 20 pe 245

egal sinus de 45 este radical din

2 supra 2 ori cosinus de 25 supra

2 ori cos de 45 este radical din

2 pe 2 ori sinus de 25 egal se

simplifică 2 și radical din 2 pe

2 și ne rămână e cosinus de 25

supra sinus de 25 Deci cotangentă

de 25 de grade și ultimul exercițiu

Săcele să simplificăm următoarea

expresie ținut de 5-alfa minus

sinus de 3 Alpha supra cosinus

de 5 Alfa plus cosinus de 3 Alpha

la numărător aplicăm formula sinus

de a minus sinus de b și obținem

2 sinus de cinci alfamino straie

alfabet 2 ori cosinus de 5 Alpha

plus 3 Alpha pe 2 aplica formula

cost de a plus coș de b și vom

avea 2 cosinus de 5 Alpha plus

3 Alpha pe 2 ori cosinus de 5-alfa

minus 3 Alpha pe 2 egal cu 2 sinus

de 2L fă pe 2 adică Alfa ori cosinus

de 8 Alfa pe doi adică 4 Alpha

supra 2 cosinus de 8 asta pe 2

4 Alpha ori cosinus de 2 L fă pe

2 L final se simplifică 2 și cozi

de 4 Alfa și ne rămâne sinus de

Alfa asupra cosinus de Alfa adică

tangență de Alfa