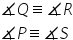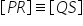Trapezul (Teorie)
Tag-uri
Partajeaza in Google Classroom

Transcript
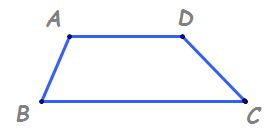
Trapezul patrulaterul care are
două laturi paralele și două laturi
neparalele se numește trapez În
figura de mai jos AB este paralelă
cu cd iar celelalte două laturi
a d și b c sunt laturile paralele
laturile paralele se mai numesc
și baze AB Se va numi baza mare
iar CD se va numi bază mică dacă
ducem o perpendiculară din d pe
ab atunci segmentul de m se va
numi înălțimea trapezului avem
următoarea clasificare a trapezului
Trapezul din imagine este un trapez
oarecare deoarece laturile neparalele
nu sunt congruente apoi mai există
trapez dreptunghic cesta este Trapezul
în care una din laturile neparalele
este perpendiculară pe baze și
un al treilea tip de trapez este
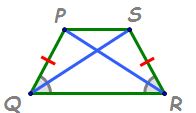
trapezul isoscel acesta este Trapezul
care are laturile neparalele congruente
Deci mq este congruentă cu PN în
continuare o să dăm o proprietate
a trapezului Într un trapez unghiurile
situate de o parte și de alta a
laturilor neparalele sunt suplementare
de exemplu măsura unghiului A plus
măsura unghiului d va fi egală
cu 180 de grade la fel și măsura
unghiului b plus măsura unghiului
c va fi egală cu 180 de grade pentru
a demonstra această proprietate
prelungim segmentul ab unghiul
acesta care sa format și pe care
îl voi nota cu x este congruent
cu unghiul D pentru că unghiul
d și unghiul x sunt unghiuri alterne
interne având în vedere că ab este
paralel cu cd iar AD este o secantă
Deci unghiul de are aceeași măsură
cu unghiul x însă unghiul x împreună
cu unghiul a formează un unghi
alungit Deci unghiul x este suplementar
cu unghiul a mai rezulta atunci
că și unghiul A și unghiul de vârf
unghiuri suplementare în continuare
o să discutăm despre proprietățile
trapezului isoscel o prima proprietate
enunțată sub forma unei teoreme
Într un trapez isoscel unghiurile
alăturate unei baze sunt congruente
avem un trapez a b c d în care
se știe că AD este congruentă cu
bc și trebuie să demonstrăm că
unghiul A este congruent cu unghiul
b și unghiul d este congruent cu
unghiul c pentru a demonstra această
teoremă o să facem o construcție
ajutătoare o să ducem perpendicularele
din de și din c pe latura ab am
construit de m și CN perpendiculare
pe ab Fie d m perpendiculară pe
AB și c n perpendiculară pe AB
pentru ca aceste două drepte sunt
perpendiculare pe AB va rezulta
că ele sunt paralele dm va fi paralel
cu c n Dar de ce este paralelă
cu AB din ipoteză a b paralelă
cu c d va rezulta atunci că acest
patrulater b c n m este un paralelogram
însă în acest paralelogram avem
un unghi drept măsura unghiului
m sau măsura unghiului n este egală
cu 90 de grade din construcție
înseamnă că acest patrulater este
dreptunghi de ce e n m va fi dreptunghi
într un dreptunghi știind că laturile
opuse sunt congruente două câte
două rezultatul Cică de m este
congruentă cu c n rezultat de m
congruent cu CN acum vom demonstra
că triunghiurile de m a și c n
d sunt triunghiuri congruente iar
din congruență acestor două triunghiuri
va rezulta că și unghiurile a și
b vor fi congruente avem Așadar
Două triunghiuri dreptunghice de
m a și c n b Până acum am arătat
că acestea au catetele de m și
c n congruente în să mai știm și
din ipoteză că AD este congruentă
cu bc pentru că a b c d este trapez
isoscel a d congruent cu b c din
ipoteză va rezulta conform cazului
de congruență ipotenuză catetă
aceste două triunghiuri sunt congruente
triunghiul DE M A este congruent
cu triunghiul cmb iar congruență
acestor triunghiul implica congruența
unghiurilor a și b pentru a demonstra
că unghiul d este congruent cu
unghiul c se prelungește latura
d c și se face o altă construcție
ajutătoare se duc perpendicularele
din a și b pe prelungirea laturii
De ce nu mai face această demonstrație
rețineți că într un trapez isoscel
unghiurile alăturate bazelor sunt
unghiuri congruente este valabilă
și reciproca acestei teoreme dacă
înfrunt trapez unghiurile alăturate
unei baze sunt congruente atunci
trapezul este isoscel am făcut
aceeași construcție ajutătoare
am dus perpendicularele din d și
c pe latura ab Așadar avem un trapez
presupunem că este un trapez oarecare
și știm că unghiul A este congruent
cu unghiul b trebuie să arătăm
că AD este congruentă cu bc demonstrația
se face asemănător cu demonstrația
teoremei 1 se arată că d c n m
este dreptunghi apoi comparăm triunghiurile
d m a și n b având în vedere că
de m este perpendiculară pe AB
și c n este perpendiculară pe AB
va rezulta că de cnm este dreptunghi
de unde rezultă că de m este congruentă
cu c n apoi în triunghiurile de
m a și c n b avem următoarele elemente
congruente d m este congruent cu
c n iar unghiul A este congruent
cu unghiul b Acest lucru se știe
din ipoteză a rezulta conform cazului
de congruență catetă unghi că triunghiul
DE M A este congruent cu triunghiul
cmb iar din această relație de
congruență va rezulta că AD este
congruentă cu bc Deci rețineți
că dacă un trapez are două unghiuri
alăturate bazei congruente atunci
trapezul este isoscel o altă proprietate
a trapezului isoscel enunțată sub
formă de aur ma numărul 3 diagonalele
unui trapez isoscel sunt congruente
avem un trapez ABCD isoscel se
știe că AD este congruent cu BC
și trebuie să arătăm că diagonalele
sunt congruente adică Ah si va
fi egală cu bd pentru a demonstra
congruență acestor două segmente
o să demonstrăm că triunghiurile
d a b și c b a sunt triunghiuri
congruente să vedem Ce elemente
congruente au acestea în primul
rând da este congruent cu b c Acest
lucru se știe din ipoteză pentru
că trapezul este isoscel am vazut
mai devreme că întru un trapez
isoscel unghiurile alăturate unei
baze sunt congruente Deci unghiul
A este congruent cu unghiul b tot
din ipoteza aceste două triunghiuri
mai au o latură comună aceasta
este latura ab Deci segmentul a
b din triunghiul d AB este congruent
cu segmentul ab din triunghiul
CBA fiind o latură comună din aceste
trei relații va rezulta conform
cazului de congruență latura unghi
latura că Triunghiul AB este congruent
cu triunghiul CBA iar de aici va
rezulta că PD este congruent cu
ac am demonstrat Așadar că între
un trapez isoscel diagonalele sunt
congruente este valabilă și reciproca
a acestei teoreme teorema numărul
patru dacă diagonalele unui trapez
sunt congruente atunci trapezul
este isoscel

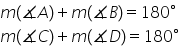
.JPG)