Triunghi dreptunghic

Categorie: Geometrie plană
Tag-uri:     triunghi dreptunghic  teorema lui Pitagora teorema inaltimii prima teorema a inaltimii a doua teorema a inaltimii  teorema catetei teorema unghiului aria triunghiului dreptunghic

Susține Lectii-Virtuale!

Triunghiul dreptunghic



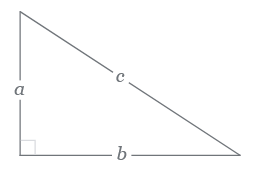
Un triunghi dreptunghic este triunghiul care are un unghi drept (π/2 radiani sau 90°). Latura opusă unghiului drept se numește ipotenuză și este cea mai mare. Celelalte două laturi se numesc catete.

Proprietățile triunghiului dreptunghic

• Suma celor două unghiuri ascuțite este egală cu 90°.(unghiurile ascuțite sunt complementare )
• Lungimea medianei corespunzătoare ipotenuzei este egală cu jumătate din lungimea ipotenuzei.
• Orice triunghi dreptunghic se înscrie într-un cerc cu centrul la mijlocul ipotenuzei.
• Orice triunghi dreptunghic are ortocentrul în vârful unghiului drept.
• Dacă un triunghi dreptunghic are un unghi cu măsura de 30 de grade, atunci cateta opusă acestui unghi este jumătate din ipotenuză.

Teoremele înălțimii



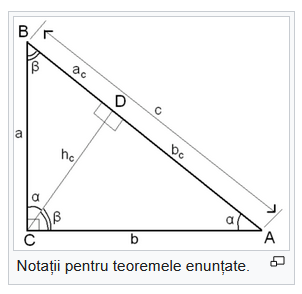
Prima teoremă a înălțimii

Într-un triunghi dreptunghic, lungimea înălțimii corespunzătoare ipotenuzei este media geometrică a lungimilor proiecțiilor catetelor pe ipotenuză.

   sau


unde CD este înălțimea corespunzatoare ipotenuzei, iar AD și BD sunt proiecțiile catetelor pe ipotenuză (v. figura de mai sus).

A doua teoremă a înălțimii

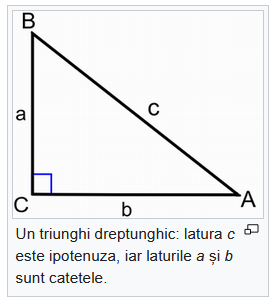
Produsul înălțimii corespunzătoare ipotenuzei cu ipotenuza este egal cu produsul catetelor, adică dacă ABC este un triunghi dreptunghic cu C=90° (v. figura alăturată), iar CD este perpendiculara pe AB. Există relația:



Teorema catetei

În triunghiul dreptunghic fiecare catetă este egală cu media geometrică dintre ipotenuză și proiecția catetei pe ipotenuză.

Fie triunghiul ABC cu C=90° și CD perpendiculara pe AB (v. figurile de mai sus). Există relația:

        sau
   

Unghiuri

Teorema unghiului de 45°

Într-un triunghi dreptunghic cu un unghi de 45° lungimea înălțimii corespunzătoare ipotenuzei este jumătate din ipotenuză.

Teorema unghiului de 30°

Într-un triunghi dreptunghic ce are un unghi de 30°, lungimea catetei ce se opune acestui unghi este egală cu jumătate din lungimea ipotenuzei.

Teorema unghiului de 15°

Într-un triunghi dreptunghic cu un unghi de 15°, lungimea înălțimii opuse unghiului de 15° este un sfert din lungimea ipotenuzei.

Formule de calcul ale ariei

Într-un triunghi dreptunghic aria este egală cu semiprodusul catetelor.

 Dacă notăm cele două catete cu c1 și c2, atunci formula pentru arie este semiprodusul catetelor:



Dacă notăm cu i – ipotenuza triunghiului și cu h – înălțimea corespunzătoare ei, atunci aria triunghiului se calculează folosind formula:



Teorema lui Pitagora



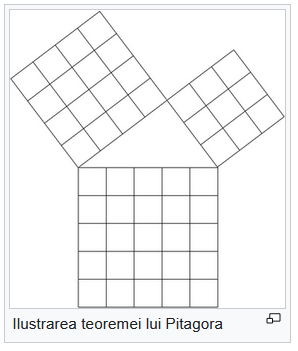
Teorema lui Pitagora: „suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei”. Aceasta poate fi reprezentată în triunghiul dreptunghic ABC, AB fiind ipotenuza, iar C unghiul drept (v. notațiile din figurile de mai sus). Teorema lui Pitagora spune că: