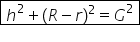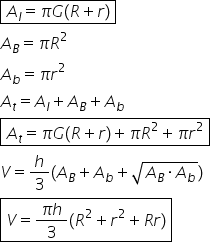Trunchiul de con circular drept (descriere, desfășurare, formule)
Tag-uri
Partajeaza in Google Classroom

Transcript
să găsim acum formulele pentru
aria laterală aria totală și volumul
unui trunchi de con circular drept
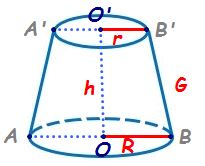
trunchiul de con circular drept
se obține prin secționarea unui
con circular drept cu un plan paralel
cu bază și prin înlăturarea conului
mic care se obține aici către vârf
și astfel obținem Iată un trunchi
de con circular drept ca elemente
observăm că avem două baze situate
în plane paralele avem aici De
fapt două cercuri și putem să notăm
aici cu oprim centrul acestui cerc
și să facem în așa fel încât să
se vadă că avem aici oprim cu o
centrul cercului mare o prim o
reprezintă de fapt înălțimea trunchiului
de con adică segmentul perpendicular
pe baza și cuprins între ele dacă
notăm aici pe cu ei acest punct
și cu b acesta atunci mai putem
să trecem aici că avem aer mare
de la raza cercului mare și aici
vom nota O primă b cu R mic raza
cercului mic deci putem să notăm
că o prim o este înălțime aer mare
am spus ce este la fericire mic
iar a b este de fapt generatoarea
trunchiului de con suprafața laterală
se desfășoară în plan după o porțiune
de coroană circulară Iată am de
prezentat aici și conul din care
face parte acest trunchi de con
și dacă desfășurăm acest trunchi
de con atunci vom obține exact
ce avem aici și anume o porțiune
de coroană circulară am reprezentată
aici și cercul de la paza mare
și cercul care reprezintă de fapt
bază mică vom mai scrie încă o
dată că o prind o reprezintă înălțimea
trunchiului de con Deci oprim o
e de fapt înălțimea trunchiului
a b reprezintă generatoarea și
mai putem să trecem aici o prim
b este raza mică raza bazei mici
de fapt și o a este raza bazei
mari voi trece aici ca avem R mic
și aici avem mare Deci o prim b
egal cu aer mic și o a egal cu
aer mare să deducem acum împreună
formula pentru aria laterală aria
laterală reprezintă de fapt aria
acestei porțiuni de coroană circulară
Cum putem să o determină pe să
facem diferența dintre aria acestui
sector de cerc din care sau obținut
conul mare și aria acestui sector
de cerc Da Din care sau obținut
conul mic de fapt facem diferența
dintre aria laterală a conului
mare și aria laterală a conului
mic să notăm Avem așa aria laterală
este egală cu voi scrie arie sector
mare minus aria sectorului mic
și acum să notăm aria laterală
este egală cu aria sectorului mare
reprezintă aria laterală a conului
circular drept acesta mare Deci
avem fie înmulțit cu raza bazei
adică iar mare înmulțit cu generatoarea
Păi generatoarea este aceasta atunci
voi nota aici cu v și atunci înseamnă
că generatoarea este vei minus
aria sectorului mic fie înmulțit
cu rază bazei adică amic înmulțit
cu generatoarea care este acum
vb dar noi vrem să exprimăm această
arie laterală fără să ne apară
aici va și vb Ce știm noi despre
aceste două segmente va și vb pe
ea este egal cu vb plus ab care
reprezintă de fapt generatoarea
trunchiului de con deci putem să
notăm așa că Va egal cu vb plus
g mare de la generatoare de aici
rezultă că aria laterală cu cât
va fi egală avem pur aer mare înmulțit
cu va adică Verde Plus gen din
care scădem aceasta fii ori urme
înmulțit cu verbe și acum desfacem
paranteza vom avea aria laterală
egală cu fiori armare orice face
mai întâi acest produs păr mare
ori adunat cupio.ro lvb orar ori
b minus pai orar mic ori vb Păi
Ce observăm iată că aici putem
să dăm factor comun pe p și pe
vb bun atunci vom avea așa că aria
laterală este egală cu pi de fapt
cred că cel mai bine ar fi să scriem
dedesubt avem peur armare origi
adunat cu Tori v b pe lângă aer
mare minus R mic și Voi păstra
doar această relație restul putem
șterge ca să avem suficient spațiu
și să vedem cum facem în continuare
în așa fel încât aria în exprimarea
ariei laterale să nu ne mai apară
segmentul vb Păi Haideți să ne
uităm puțin la această figură și
chiar o să unesc și vecu oprim
ca să ne facem cât de cât o idee
acest plan este paralel cu acesta
dacă Privim și planul determinat
de punctele o A atunci la ce ne
gândim Păi când două plane paralele
sunt intersectate de un al treilea
plan înseamnă că dreptele de intersecție
sunt paralele și aici dreapta de
intersecție este o prim b și aici
Este o A deci avem că o prim b
paralelă cu o a cu alte cuvinte
triunghiul v o prim b este asemenea
cu triunghiul b o a și n triunghiul
V8 prim b asemenea cu triunghiul
v o a și vom obține un raport de
asemănare v b supra va este egal
cu R mic supra aer mare atenție
noi vrem să le exprimăm pe verbe
în funcție de aer mare R mic sau
în funcție de gen cum facem acest
lucru de vreme ce am găsit acest
raport Păi nu vom scoate pe bebe
din această proporție ca atunci
o să le exprimăm în funcție de
A deci nu o să câștigăm mare lucru
însă putem să facem proporții derivate
pentru că Iată va minus vba minus
vb.net de de fapt segmentul a b
adică generatoarea trunchiului
de con rezultă de aici facem următoarea
proporție de sub va minus vb cu
cât este egal Păi avem aer mic
supra aer mare minus a r mic și
am obținut că v b supra vei minus
v b reprezintă de fapt generatoarea
trunchiului de con egal cu R mic
super mare minus thermique acum
îl exprimăm pe bebe din această
proporție stau mai vine devreme
si noi avem nevoie aici de produsul
vb ori aer mic păr mare Pardon
minus thermique Iată putem să înmulțim
aici pe diagonală De ce avem rezultă
din proporție că v b înmulțit cu
R mare minus termic egal cu g aur
are mic și acum venim și înlocuim
aria laterală voi scrie aici este
egală cu ori urma are orice adunat
cu înmulțit cu și avem acest produs
Iată Care este exprimată aici prin
g mare orar mic g mare ori R mic
de Unde putem să găsim foarte ușor
formula pentru aria laterală rezultă
că aria laterală este egală cu
orgi pe lângă R Mare plus R mic
R Mare plus termic și vreau să
trecem această relație mai departe
ca să separăm cât de cât și astfel
am de terminat formula pentru aria
laterală a trunchiului de con circular
drept să găsim acum și aria totală
Deci șterge tot ce am scris aici
Voi păstra doar formula pentru
laterală pe care am găsit o împreună
Deci avem această formulă și vrem
să determinăm acum formula pentru
aria totală e simplu aria totală
este egală cu aria laterală plus
aria bazei mari prismei b mare
plus aria bazei mici aria bazei
mari știm Cât este avem aici la
asta deci să înlocuim aria totală
este egală cu ce avem aici adică
aria laterală adunată cu aria bazei
mari avem fie orar mare la pătrat
plus aria bazei mici adică fie
ori urma creată la pătrat pentru
volum să știți că formula pentru
volum este identică cu formula
pe care am întâlnit o la trunchiul
de piramidă regulată Deci avem
înălțimea supra 3 și în paranteză
avem aria bazei mari plus aria
bazei mici plus radical din aria
bazei mari aria bazei mici și acum
să înlocuim vom avea că volumul
formula pentru volum este egală
cu înălțimea supra 3 pe lângă De
fapt chiar o să scriem cu alb mai
întâi ca voi o să te duci în forma
finală Deci volumul este egal cu
înălțimea supra 3 pe lângă aria
bazei mari orar mare la pătrat
plus aria bazei mici ior urme la
pătrat plus si vom obține aici
avem radical din aria bazei mari
adică fuhrer mare la pătrat înmulțit
cu aria bazei mici pai orar mic
la pătrat cât vom obține sub radical
mai avem așa pe la a doua Deci
pai o să iasă de sub radical la
fel și s mare la fel și aer mic
Deci în loc de acest radical o
să șterg și o să trecem exact ce
am scris aici Adică pur aer mare
ori aer mic și acum rezultă că
formula pentru volum este următoarea
putem să dăm factor comun pe Deci
avem fie ori H supra 3 pe lângă
aer mare la a doua plus R mic la
a doua plus produsul dintre a mare
și a mic și astfel am de terminat
formula pentru aria laterală pentru
aria totală și pentru volumul unui
trunchi de con circular drept