Trunchiul de piramidă (definiție, elemente)

avem aici o piramidă patrulateră

pe care o secționam după un plan

paralel cu baza secțiunea obținută

este această figură geometrică

Care este asemenea cu baza piramidei

și de remarcat este faptul că oriunde

am așeza acest plan fie foarte

aproape de vârf fie din ce în ce

mai aproape de bază vom obține

întotdeauna două corpuri geometrice

Ce anume o piramidă mai mică și

partea de jos se numește trunchi

de piramidă Iată Deci avem aici

să se vadă mai bine piramida mai

mică și ce avem aici la bază se

numește trunchi de piramidă să

vedem acum Care sunt elementele

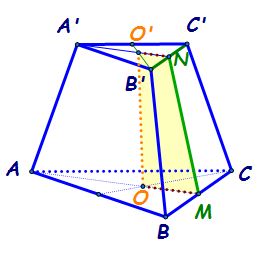
trunchiului de piramidă trunchiul

de piramidă a are două baze paralele

Iată baza a b c d este paralelă

cu baza a prim b prim c prim D

prim și poligoanele a b c d și

a prim b prim c prim D prim sunt

poligoane asemenea DC reținem că

bazele sunt poligoane asemenea

și sunt situate în plane paralele

fețele laterale De exemplu a prim

b prim b a c sunt sunt trapeze

Deci reținem și acest fapt că fețele

laterale sunt trapeze același lucru

se întâmplă și în cazul unui trunchi

de piramidă triunghiulară vom avea

bazele triunghiuri asemenea iar

fețele laterale vor fi tot trapeze

avem aici și a b muchia bazei mari

a prim b prim muchia bazei mici

a prim a sau b prim b oricare dintre

aceste patru muchii se numesc muchii

laterale înălțimea în triunghi

de piramidă Iată reprezintă segmentul

cuprins între cele două baze și

perpendicular pe nu are importanță

unde trecem înălțimea în triunghi

de piramidă știind că între un

trunchi de piramidă oricare două

înălțimi sunt congruente ca să

desenăm un trunchi de piramidă

e mai simplu să pornim de la piramida

din care acesta face parte a astfel

avem piramida patrulateră V a b

c d timp de joacă Dacă secționam

piramidă cu un plan paralel cu

bază vom obține un trunchi de piramidă

atenție trunchiul de piramidă moștenește

proprietățile piramidei din care

provine a astfel dacă ni se dă

o piramidă patrulateră regulată

atunci o să ne rezulte un trunchi

de piramidă patrulateră regulată

și acum să vedem planul Care este

paralel cu planul bazei și să construim

trunchiul de mami Da deci vom trece

acest segment apoi pe acesta pe

acesta cu alte cuvinte construim

bază mică a trunchiului de piramidă

și pe acesta vom colora tot cu

portocaliu și muchiile laterale

Da precum și muchiile bazei a b

c d și a trup tine un trunchi de

piramidă pe care Haideți să îl

denumim înainte de aceasta să facem

în așa fel încât să nu se mai vadă

acest plan bun și avem aici a prim

b prim c prim D prim Deci avem

trunchiul de piramidă patrulateră

regulată ABCD a prim b prim c prim

D prim a cu fețele laterale sunt

trapeze isoscele congruente deci

putem să nu uităm că aceste muchii

laterale sunt congruente și fețele

laterale lipit sunt trapeze isoscele

congruente bazele sunt pătrate

asemenea Deci trecem aici că pătratul

a b c d este asemenea cu pătratul

a prim b prim c prim D prim când

vorbim de înălțimea întrun trunchi

de piramidă atunci să știți că

în general alege în segmentul care

se află între cele două baze și

se află pe înălțimea piramidei

atunci să construim înălțimea acestei

piramide V a b c d cu alte cuvinte

construim mai întâi centrul cercului

circumscris bazei Deci trasăm intersecția

diagonalelor vom trece aici punctul

O bun Vio este înălțime în asta

piramidă și chiar o să trecem și

intersecția înălțimii piramidei

cu bază mică cu alte cuvinte avem

aici să o facem tot punctat trebuie

să trasăm centrul cercului circumscris

bazei mici care ia de intersectează

înălțimea v o 8 pentru un punct

pe care o să îl notăm aici o prim

nu știu dacă se vede prea bine

că e mai oprim bun oprim o este

înălțime în trunchiul de piramidă

Deci Haide să notăm că o prim o

este înălțime în trunchiul de piramidă

apotema trunchiului de piramidă

este înălțimea unei fețe laterale

și de obicei alegem ca apă Ema

a trunchiului de piramidă segmentul

aflat pe apotema piramidei și cuprins

între cele două baze Deci vrem

să construim apotema piramidei

mai întâi trecem aici și punctul

m Care este mijlocul segmentului

BC și atunci dacă unim pe V cu

m v e m este apotema a piramidei

avem aici punctul Deci aici avem

B prim dar aici avem punctul M

prin intersecția dintre b prim

c prim și b m chiar o să șterg

aici pe b prim ca să trecem ceva

mai departe Deci avem aici de prim

bun de vreme si mie este perpendiculară

pe BC avem aici un unghi de 90

de grade cu b prim c prim paralelă

cu bc înseamnă că și aici avem

tot un unghi de 90 de grade cu

alte cuvinte apotema trunchiului

de piramidă este m prim e și chiar

putem să notăm apotema trunchiului

de piramidă se notează cu a t r

de la trunchi este egală cu m prim

m apotema bazei mari a trunchiului

de piramidă este perpendiculară

adusă din centrul cercului circumscris

pe o muchia bazei știm deja că

aceasta este o m Deci trecem aici

că apotema bazei mari dacă ne referim

la trunchiul de piramidă o să trec

aici un b mare de la apotema bazei

mari este om Deci perpendiculara

dusă din centrul cercului circumscris

bazei pe o muchie a bazei și acum

apotema bazei mici care se notează

cu a indice b mai cred că deja

știți care este Trebuie să ducem

perpendiculară din o prim b prim

c prim adică vorbim de 8 prim m

prim și să o trasăm bun aceasta

este și să o trecem Și aici este

apotema bazei mici o prim m prim

cu alte cuvinte între un trunchi

de piramidă Iată am șters piramida

și Haideți acum să ștergem și aceste

linii care sunt în plus Care sunt

elementele unui trunchi de piramidă

să facem și aici ca avem 90 de

grade avem așa înălțimea trunchiului

de piramidă Care este oprim o apotema

trunchiului de piramidă Care este

m prim m apotema bazei mari care

este om și apotema bazei mici care

este o prim m prim întru un trunchi

de piramidă triunghiulară regulată

avem Iată o prim o este înălțimea

trunchiului de piramidă m prim

m este apotema trunchiului de piramidă

o prim m prim este apotema bazei

mici și 1000 este apotema bazei

mari