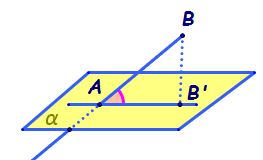
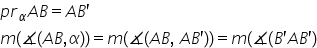Unghiul unei drepte cu un plan

în continuare să stabilim cum determinăm

măsura unghiului format de o dreaptă

cu un plan dacă dreapta este perpendiculară

pe plan atunci lucrurile sunt simple

dreapta d perpendiculară pe planul

alfa atunci cum vorbim de perpendicularitate

înseamnă că măsura unghiului făcut

de dreapta d și planul alfa Câte

grade are 90 de grade avem aici

o dreaptă perpendiculară pe un

plan dacă însă dreapta nu e perpendiculară

pe plan atunci măsura unghiului

format de un plan și o dreaptă

ce nu e perpendiculară pe plan

este egală cu măsura unghiului

format de acea dreaptă cu proiecția

ei pe plan și idee să vedem și

desenul iar dreapta d nu este perpendiculară

pe planul alfa A bine în această

situație măsura unghiului format

de dreaptă și de plan este de fapt

măsura unghiului format de dreapta

D cu proiecția a Pe plan Păi proiecția

pe planul alfa a dreptei d este

dreapta a d prim e ușor de văzut

și atunci rezultă că măsura unghiului

format de dreapta d și planul alfa

iar nu o să scriu dreapta de o

să o numesc dreapta AB o putem

numi și astfel Deci măsura unghiului

format de dreapta a b și planul

alfa este de fapt măsura unghiului

format de dreapta a b și a b prim

a b și a d prim cu alte cuvinte

ce unghii avem Păi a dreapta a

b și a b prim formează unghiul

b a b prim adică acest unghi venim

aici notăm egal cu măsura unghiului

b a d atenție când vorbim de unghiul

făcut de două drepte concurente

știind că obținem de fapt două

măsuri de unghiuri această măsură

și această măsură însă prin convenție

alege măsura mai mică în cazul

nostru această măsură pentru fiecar

că acest unghi este mai mare decât

are măsura mai mare decât acesta

poate cuvinte când vorbim de o

măsura unghiului format de o dreaptă

cu un plan vorbim de fapte măsura

unghiului format de dreapta respectivă

cu proiecția ei pe plan ce se întâmplă

însă Dacă dreapta e paralelă cu

planul Păi aplicăm aceeași regulă

dată aici Deci ce vom obține Iată

dreapta a b paralelă cu planul

alfa am notat și aici proiecția

aceste drepte Pe plan este dreapta

a prim D prim cele două drepte

AB și a prim b prim sunt paralele

trec aici a b paralelă cu a prim

b prim atunci conform regulii învățate

anterior rezultă că măsura unghiului

făcut de dreapta a b și planul

alfa dreapta AB și planul alfa

este de fapt egală cu măsura unghiului

făcut de dreapta a b și proiecția

a Pe plan Deci dreapta b și dreapta

a prim b prim și c unghi vom ce

măsură vom obține Păi cum avem

două drepte paralele ia ta notat

aici înseamnă că avem 0 grade dacă

însă dreapta este inclusă în plan

atunci ea de dreapta b este inclusă

în planul alfa tot așa conform

regulii învățate înseamnă că măsura

unghiului făcut de dreapta d și

planul alfa e de fapt egală cu

măsura unghiului făcut de dreapta

AB de proiecții pe plan însă Cum

dreapta este inclusă în plan înseamnă

că proiecția a pe plane kiar dreapta

însăși Deci măsura unghiului făcut

de dreapta b și te ia în să trec

aici tot dreapta b alte cuvinte

obținem tot așa 0 grade să facem

acum o aplicație se dă dreptunghiul

ABCD m a e perpendiculară pe planul

a b c d m perpendiculară pe planul

abc cu alte cuvinte perpendiculară

pe planul ABCD pentru ca aceste

patru puncte sunt coplanare și

lungimile segmentelor ca în figură

avem m a a centimetri AB tot amic

centimetri BC a migra Adica din

3 cm și putem Să considerăm că

punctul că numărul A pardon este

un număr rațional pozitiv să determinăm

măsura unghiului format de Ema

și planul abc deci de dreapta m

a și planul a b c și planul a b

c d cu alte cuvinte Păi cum este

dreapta m n față de planul abc

spune aici perpendiculară de ceai

de să trecem pentru punctul a mic

devreme cm a e perpendiculară pe

planul a b c rezultă că măsura

unghiului făcut de această dreaptă

m a și a chest plan a d c este

de 90 de grade avem dreaptă perpendiculară

pe plan al doilea subpunct sub

punctul b mic să determinăm acum

măsura unghiului format de dreapta

a m b și planul a b c Iată avem

aici dreapta m b și planul a b

c d cum determinăm acum unghiul

format de această dreaptă cu acest

plan Păi trebuie mai întâi să vedem

care este proiecția dreptei m b

Pe planul a b c d și e foarte simplu

de văzut că proiectând punctul

M Pe planul a b c d obținem punctul

A proiectând punctul B pe acest

plan obținem punctat punctul B

Deci proiecția dreptei MB pe acest

plan este de fapt dreapta a b și

Haideți să notăm că proiectând

dejun Natasha proiecția Pe planul

abc a punctului m este punctul

A proiecția pe același plan abc

a punctului b este tot punctul

B pentru că punctul B face parte

din acest plan deci de aici rezultă

că proiecția Pe planul abe De ce

a dreptei m b este si dreaptă este

dreapta AB Păi ce vom obține atunci

înseamnă că unghiul făcut de această

dreaptă m b cu planul a b c d este

de fapt unghiul făcut de această

dreaptă m d cu dreapta a b adică

vorbim de acest unghi și să notăm

rezultă că proiecția pardon că

măsura unghiului format de dreapta

m b cu planul abc adică exact ce

se cere aici un enunț este egală

cu măsura unghiului făcut de dreapta

m d cu dreapta a b și c unghi obtuz

m Cum se numește unghiul trasat

aici cu roșu m d a măsura unghiului

m d a pun și acum rămâne de făcut

decât să determinăm măsura acestui

unghi ce Observă În triunghiul

m a b avem m a congruent cu AB

și ce fel de triunghi avem pe m

a este perpendiculară pe planul

a b c d și a b este inclusă în

acest plan înseamnă că m a e perpendiculară

pe AB deci putem să trecem aici

ca avem un unghi de 90 de grade

și haide să notăm că avem așa m

a perpendiculară pe planul a b

c d avem aici planul a b c d dreapta

AB este inclusă în acest plan a

b c d sau a b c putem să notăm

și așa rezultă că m a este perpendiculară

pe a b cu alte cu înseamnă că avem

acest unghi de 90 de grade Deci

rezultă că avem triunghiul m a

b m d cu măsura unghiului A de

90 de grade Deci avem un triunghi

dreptunghic și mai cum este el

este isoscel pentru că m a congruent

cu AB m a egal cu a b putem să

trecem în continuare a mic cm Deci

având aici un triunghi dreptunghic

isoscele înseamnă că măsura acestui

unghi precum și a acestuia este

de 45 de grade Deci veniți și notăm

că măsura unghiului Cum se numește

m b a m b a este de 45 de grade

și acum haide să subliniem am avut

De determinat măsura acestui unghi

care de fapt cu măsura unghiului

MBA și atât ca am găsit ca avem

45 de grade sub punctul c mic să

determinăm măsura unghiului format

de dreapta m d și planul abc adică

planul a b c d tot așa care este

proiecția dreptei m d Pe planul

a b c d proiecția punctului m pe

plan este punctul A punctul d aparține

planului asta înseamnă că notăm

direct proiecția de sub punctul

c mic proiecția Pe planul abc a

dreptei m d este de fapt dreapta

ad Ce rezultă de aici că măsura

unghiului Deci rezultă în continuare

că măsura unghiului format de dreapta

m d și planul ABC este de fapt

egal cu măsura unghiului format

de dreapta m d și proiecția ei

pe plan Care este dreapta a d Iată

aici A deci ce unghii vom avea

dreapta m d și a d formează acest

unghi adică m d a egal cu măsura

unghiului m de pat și să determinăm

acum măsura acestui unghi În primul

rând Ce fel de triunghi este m

a d pe avem tot un triunghi dreptunghic

unghiul a are 90 de grade explicația

este asemănătoare cu cea a făcut

aici când am arătat că unghiul

m ab are 90 de grade Deci notăm

direct că m este perpendiculară

pe a d asta înseamnă că avem triunghiul

m a d cu măsura unghiului A de

90 de grade ce mai cunoaștem în

acest triunghi m a d avem aici

A centimetri Care este lungimea

segmentului a d si este a b c d

este un dreptunghi și avem aici

că bc este are Pardon A radical

din 3 cm înseamnă că și aici avem

tot a radical din 3 centimetri

Deci cunoaștem și lungimea acestei

catete și lungimea acestei catete

Cum putem să determinăm măsura

acestui unghi aplicăm o funcție

trigonometrică de vreme ce cunoaștem

lungimile catetelor e mai simplu

să aplicăm o tangentă sau cotangenta

Deci avem tangentă de unghiul m

d a este egală cu raportul dintre

lungimea catetei opuse unghiului

Deci Ema și lungimea catetei alăturate

unghiului adică ad și înlocuim

și vom avea așa ma are Ami centimetri

Deci avem a supra a d are a radical

din 3 dacă simplificăm prin a a

este un număr rațional diferit

de 0 atunci vom obține 1 supra

radical din 3 raționalizăm și vom

avea radical din 3 pe 3 ce măsură

are unghiul m de a astfel încât

tangenta acestui unghi să ne dea

radical din 3 pe 3 Păi tangentă

de 30 de grade este egală cu radical

din 3 pe 3 d c restul Dacă măsura

unghiului m d a este de 30 de grade

și putem să subliniem iar Teodor

am să determinăm măsura unghiului

făcut de dreapta m d planul abc

am obținut este egală cu măsura

unghiului Mda adică avem 30 de

grade figura aceasta nu este singura

metodă prin care putem obține Câte

grade are acest unghi beată daca

aplicam În triunghiul m a d teorema

lui Pitagora atunci aici în fi

obținut că avem 2-a centimetri

și atunci de vreme ce această catetă

are lungimea egală cu jumătate

din lungimea ipotenuzei conform

reciprocei teoremei unghiului de

30 de grade înseamnă că măsura

acestui unghi este întradevăr de

30 de grade