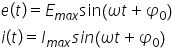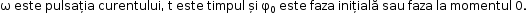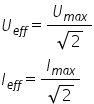Valori momentane şi valori efective ale fluxului, tensiunii şi intensităţii.

În ce dată patra lecție de curent

alternativ vom discuta despre mărimile

caracteristice ale curentului alternativ

primul set de mărimi despre care

discutăm sunt mărimile momentane

sau instantanee Care sunt mărimile

ce depinde timp și pentru care

în consecință avem o dependență

explicită de timp în această prima

formulă vedeți mărimea momentană

a fluxului magnetic care a fost

dedusă și folosită în lecția trecută

valoarea maximă a acestui flux

magnetic în lecția trecută a fost

demonstrată să fie egală cu produsul

dintre inducția magnetică și suprafața

circuitului electric și această

valoare maximă este înmulțită cu

o un cosinus de un argument de

pe De ce depinde de timp în acest

grafic cu verde de Puteți vedea

această funcție a fluxului Magnetic

de argumentul Omega tecusa ții

muncită cu timp fie 0 Nu nu a fost

introduși folosit în lecția trecută

pentru că nu era foarte relevant

în contextul acelei discuții Dar

în general putem avea un factor

și 0 care este independent de timp

și se numește fază inițială prin

definiție fie 0 este valoarea argumentului

întregul argument la momentul t

0 egal cu 0 în lecția trecută am

demonstrat Care este formula pentru

mărimea nomentana a tensiunii electromotoare

induse plecând de la această ecuație

pentru fluxul pentru mărimea momentană

a fluxului magnetic și am găsit

că tensiunea electromotoare indusă

depinde de timp pentru o funcție

sinusoidal de ce avem un sinus

de același argument înmulțit cu

o valoare maximă care a fost găsită

ca fiind egală cu b so romega sau

dacă doriți este egală cu pulsația

Omega înmulțită cu valoarea maximă

a fluxului magnetic din această

ecuație pentru tensiune electromotoare

indusă putem foarte ușor să găsim

ecuația pentru curentul electric

induse de ten De ce el va fi o

valoare maximă a curentului în

dus înmulțită cu aceeași funcție

sinus de omega-3 plus si 0 Iar

e m valoarea maximă a curentului

Este legată de valoarea maximă

a tensiunii electromotoare prin

legea om după cum am spus fie zero

se numește faza inițială și este

faza totală a funcției sinus sau

cosinus calculată la momentul t

egal cu 0 Deci acest întreg argument

al funcției sinus sau cosinus omega-3

plus fie 0 este se numește faza

totală și are o dependență de timp

Bineînțeles dacă ne uităm cu atenție

la variația în timp acestei fază

totale adică calculăm Delta fi

care prin definiție de faza la

momentul t plus un interval de

el tot a minus valoarea la momentul

t observăm că a este egală cu Omega

3 Omega Delta t pentru că fi 0

se simplifică prin scădere Deci

pulsația curentului alternativ

este variația fazei totale în unitatea

de timp deci în contextul curentului

alternativ pulsația Omega e viteza

de variație a fazei totale a curentului

sau a tensiunii electromotoare

în lecția trecută când am discutat

despre Omega am văzut că el era

viteza de rotație a circuitului

electric în care are loc fenomenul

de inducție electromagnetică Dar

acest fenomen de inducție electromagnetică

are loc în tu de obicei în turbina

centrale electrice care generează

curentul alternativ si ajunge la

prizele noastre și felul în care

funcționează turbina într o centrală

electrică are mai puțină relevanță

pentru un consumator de curent

electric luat direct de la priză

în casa dumneavoastră De ce mai

relevant să definim pulsația curentului

alternativ în funcție de parametrii

curentului așa cum îl găsim în

priză și atunci găsim această definiție

opcom un comentariu Apropo de faza

fie 0 dacă ne uităm la dependența

temporală enunțului e de t în albastru

observăm că e la momentul t egal

cu zero este egal cu e m înmulțit

cu sinus de fizzer și aceasta este

valoarea graficului e d t în punctul

t egal cu 0 d e Maximul cu SIM

de sinus de faza inițială este

valoarea acestui acestei dependențe

temporale ale curenților și tensiunilor

alternative se poate observa direct

vizualul cu un instrument numit

osciloscop ce vedeți în această

imagine este un osciloscop conectat

la un element de curent alternativ

și se poate vedea direct pe ecranul

lui forma unui concurent sau în

ai tensiune în funcție de cum este

cuplat și ce măsură scuzați următorul

set de mărime fac de mărimi ce

descriu curentul alternativ se

numesc mărim efectiv să le introducem

pas cu pas datorită periodicității

funcției sinus sau și a funcției

cosinus putem spune că Spre exemplu

intensitatea momentană curentul

la momentul te va fi egală cu minus

intensitatea momentană la momentul

t plus perioada împărțită la doi

de aici rezultă că atunci când

când vom calcula media pe o perioadă

lungă a curentului momentan vom

obține 0 De ce Haideți să vedem

de ce se întâmplă asta Deci ce

vedeți aici în primul rând cu albastru

Deci vă rog să vă uitați la funcția

cu albastru care este sinus de

omega-3 bineînțeles am ales sinus

de omega-3 pentru că e de ten este

egal cu un maxim sinus de Omega

3 în care nu am mai scris faza

inițială fie zero Așa dacă vă uitați

la această funcție veți vedea că

ea are o perioadă Deci perioada

unei funcții este momentul după

care ori valoarea temporală după

care funcția se repetă în cazul

nostru veți vedea că perioada este

bineînțeles 6 și 8 care corespunde

lui 2pi Deci aceasta este perioada

t există bineînțeles un o valoare

tp2 Deci Linia roșie va arată în

momentul în care funcția ajunge

la timpul egal cu perioada împărțită

la 2:00 după care se ia se repetă

cu semnul minus și deci dacă Considerăm

oricare punct de Să considerăm

oricare punct pe partea pozitivă

a lui sinus de omega-3 ia corespunde

unei anumite valori anumite valori

Omega tem că și aici poate se vede

mai bine aici Omega Și dacă ne

ducem peste te supra 2 la un moment

Simetric Deci avem patru diviziuni

aici mă duc la 1 2 3 4 aici vom

avea omega-3 plus tp2 observăm

că punctul care corespunde acestui

punct de pe grafic va avea aceeași

amplitudinea curentului dar cu

semnul minus Deci avem și minus

e Deci pentru fiecare punct pe

partea pozitivă Luis de Omega te

există un punct corespunzător pe

partea negativă care are aceeași

magnitudinea curentului dar semne

Gate Deci când vom aduna ca să

calculăm media obținem 0 media

curentului va fi să putem demonstra

acest lucru chiar și plecând la

definiția mediei valoarea medie

a unei funcții f de x între parametrii

în între valorile X1 și X2 ale

argumentului x este aria de sub

graficului f de x între X1 și X2

împărțită la x 2 minus fixul matematic

scris media lui ef este aria funcției

f între X1 și X2 împărțit la x

2 minus fixul dar dacă ne uităm

din nou la curba albastră a lui

sinus de Omega observăm că avem

pentru o perioadă suficient de

lungă de timp fiecărui loeb sau

fiecărei zone pozitive corespunde

o zonă negativă această zonă va

avea o arie pozitivă iar această

zonă va avea Oare negativă dar

egal Deci când vom aduna vom obține

același lucru și anume că media

intensității este zero la fel media

tensiunii este de din acest motiv

nu putem folosi direct media pentru

aceste mărimi pentru a caracteriza

circuitele de curent alternativ

și tocmai din acest motiv să introduc

așa numitele valori medii efective

care sunt definite ca rădăcina

pătrată a mediei pătratului valorii

momentan deci practic ce facem

Nu calculăm media lui e și întâi

ridicăm pe la pătrat și calculăm

media lui bineînțeles ca să nu

obținem valori de pătratul unui

curent după aceea extragem radical

de ce sau Care este ideea principală

pe foarte simplu în momentul când

ridicăm sinus de Omega te la pătrat

Deci din nou când ridicăm curentul

e la pătrat ridicăm atât si in

față m dar în principale de câmp

sinus de omega-3 pătrat sinus de

omega-3 la pătrat va avea loc pozitivi

pătratul lobului pozitiv va fi

pozitiv dar pătratul lobului negativ

va fi și el la rândul lui pozitiv

De ce vom avea o serie de la pozitiv

și atunci media nu va mai fi 0

si va avea o valoare pozitivă definită

a acestui parametru acestui parametru

Haideți să vedem care este această

valoare medie efectivă Deci luăm

e pătrat de tecar este m pătrat

sinus pătrat de omega-3 folosind

următoarea formulă trigonometrică

2 sinus pătrat de Alfa este egal

cu 1 minus cosinus de 2 Alfa scuzați

avem această formulă în acest grafic

care a devenit destul de încărcat

dar în acest grafic puteți Observa

cu verde funcția cosinus de 2 puncte

și Ce observăm este care aceeași

proprietate ca și sinus de omega-3

pentru fiecare lob sau zonă negativ

există o zonă pozitivă egală ca

valoare Deci când ne vom când vom

începe să le adunăm vom obține

zerouri vor simplifica una în perechi

Deci media lui cosinus de 2 puncte

pe o perioadă suficient de lungă

de timp va fi 0 și Deci e efectiv

Care este Deci revenind prin mediere

acest termen dispare și atunci

e pătrat mediul va fi egal cu e

m pătrat împărțit la 2 extrage

radicalul Deci valoare efectivă

medie a curentului alterne este

valoarea lui Maxim împărțit la

radical din 2 la fel și tensiune

efectivă valoarea maximă împărțit

la radical din doi în afară de

faptul că dau o estimare a valorilor

medii ale curentului și tensiunii

aceste valori medii efectiv mi

iau și eu o altă semnificație foarte

importantă despre care discutăm

acum Deci dacă ne uităm la definiția

valorii medii efectiv m a curentului

electric indus Care este aceea

aceasta dacă ridicăm la pătrat

și înmulțim cu rezistența din curentul

nostru din circuitul nostru vedem

că r e pătrat efectiv este egal

cu a r i pătrat magic de aici putem

trage concluzia care se poate demonstra

și mai riguros decât atât dar această

demonstrație simplă vă vă sugerează

imediat această proprietate care

o voi citi acum intensitatea efectivă

e efectivă a curentului alternativ

ai de te egală cu valoarea curentului

continuu e un anumit conținut curent

continuu care traversând același

rezistor În același interval de

timp generează aceeași cantitate

de energie termică ca și e Deci

acest e efectiv poate fi înlocuit

în poate înlocui edte din punct

de vedere al efectului termic al

curentului alternativ al bineînțeles

fiind un curent continuu Deci prin

aceste valori medii efectiv am

găsit valoarea unui curent continuu

el trebuie să fie de această mărime

efectiv pentru a produce aceleași

efecte în circuitul nostru alternativ

ca și edp