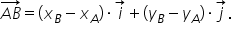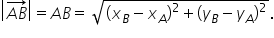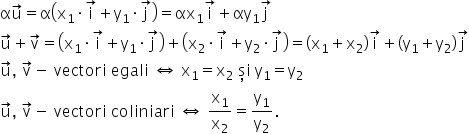Vectori în reper cartezian
Tag-uri
Partajeaza in Google Classroom

Transcript
în acest clip poți să facem câteva
exerciții în care vom exprima niște
Vector cu ajutorul versorilor e
și j avem un reper cartezian următoarele
puncte a de coordonate 1 2 b de
coordonate minus 2 3 și c de coordonate
2 minus 1 la punctul a se cere
să determinăm coordonatele vectorului
o a plus OB plus oc Adică trebuie
să scriem expresia analitică a
acestui Vector cu ajutorul versurilor
e și j la b se cere să determinăm
coordonatele vectorului 3-a b plus
4 AC plus BC iar la punctul C trebuie
să calculăm modulul vectorilor
AB și BC am scris alăturată aceste
două formule pe care o să le aplicăm
în acest exercițiu și pe care le
am văzut în clipul anterior vectorul
ab are următoarea expresie analitică
x b minus x a ori y plus y b minus
y origyn Deci începem întotdeauna
cu al doilea punct cu abscisa punctului
b apoi modulul vectorului AB este
radical din x b minus x la pătrat
plus y b minus y a la pătrat începem
Așadar cu punctul A pentru a determina
coordonatele acestui Vector vom
scrie mai întâi fiecare Vector
cu ajutorul versurilor e și g Punctul
o este originea sistemului de axe
și el are coordonatele 0 și 0 să
vedem mai întâi vectorul o a aplicăm
prima formulă începem cu abscisa
celui de al doilea punct adică
cu abscisa punctului a x ul lui
a este 1 pixul lui este 0 ori e
plus ordonata punctului a este
2 ordonata punctului o este 0 Orange
unu ori este e plus 2 j Așadar
coordonatele vectorului o a sunt
1 și 2 adică acești coeficienți
adversarilor i și j să exprimăm
acum vectorul OB cu ajutorul versurilor
e și j începem cu al doilea punct
exista punctului b este minus 2
exista punctului o este 0 ori Y
plus ordonata punctului b este
3 ordonata punctului o este 0 egal
minus 2x plus 3 j iar vectorul
oc abscisa punctului c este 2 exciza
punctului o este zero ordonata
punctului c este minus 1 ordonata
punctului o este 0 egal cu doi
i a minus j acum adunăm acești
trei vectori suma se va face pe
componente o a plus OB plus oc
egal vom înlocui fiecare Vector
cu expresia analitică scrisă mai
sus Avem i plus 2 j apoi o b este
minus 2 plus 3 j o să pun și aici
o paranteză ca să evidențiem mai
clar fiecare Vector Plus o Ce este
2 e minus Z egal acum adunăm coeficienții
verișorului e Avem 1 minus 2 plus
2 Adică 1 urmează apoi 2 j plus
3 5 minus 1 4 plus 4 J Așadar expresia
analitică a vectorului sumă o a
plus OB plus oc este e plus 4 j
cu alte cuvinte coordonatele acestui
Vector sunt 1 și 4 am terminat
punctul A continuăm cu B la b trebuie
să determinăm coordonatele vectorului
3-a b plus 4 AC plus bc mai întâi
vom scrie expresiile analitice
ale vectorilor AB AC și BC începem
cu vectorul AB aplicăm prima formulăm
pixul lui b este minus 2x lui a
este 1 ori e plus y cu a lui b
este 3 y a lui A este 2 ori Z egal
cu minus 3x plus j vectorul AC
începem cu acciza punctului c 2-a
minus abscisa punctului a 1 ori
Y plus ordonata punctului Ce este
minus 1 iar ordonata punctului
a este 2 ori Z egal e minus 3 j
și vectorul BC fixul lui Ce este
2x ul lui b este minus doi Deci
avem minus minus 2 ori y plus y
cu lui c este minus 1 egal Punctul
lui b este 3 ori j egal 2-a minus
minus doi este 4 minus 1 minus
3 minus 4 j și acum să scrie în
vectorul 3 ab plus 4 AC plus bc
egal cu 3 pe lângă în loc de ab
o să scrie expresia analitică de
mai sus minus trei y plus z plus
4 pe lângă în loc de ace avem e
minus 3 j și plus bc adică patru
e minus 4 j egal desfacem parantezele
acest scalar se distribuie la fiecare
vers ore în parte o să avem A minus
9 e plus 3 j plus 4 minus 12 j
plus 4 minus 4 J egal minus 9 plus
patru este minus 5 plus 4 minus
1 Deci avem minus e apoi 30 minus
12 este minus 9 minus 4 minus 13
j Iată am obținut și coordonatele
acestui Vector acestea sunt minus
unu și minus 13 și la punctul ce
trebuie să calculăm modulul vectorilor
AB și BC o să încep cu modulul
vectorului bc și avem radical din
pixul lui c este 2 minus x lui
b este minus 2 o să scriu direct
plus 2 la pătrat plus y cu a lui
C este minus 1 minus y cu a lui
b este 3 la pătrat egal cu radical
din 2 plus 2 4 la a doua 16 plus
minus 4 la a doua 16 egal cu radical
din 2 ori 16 și egal cu 4 radical
din 2 modulul vectorului ab vă
rămâne temă Trebuie doar să aplicați
prima formulă deci este foarte
simplu gata

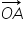 se descompune după direcțiile date de cei doi versori astfel:
se descompune după direcțiile date de cei doi versori astfel: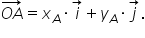
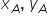 se numesc coordonatele carteziene ale punctului A sau coordonatele vectorului
se numesc coordonatele carteziene ale punctului A sau coordonatele vectorului 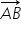 se descompune după direcțiile date de cei doi versori astfel:
se descompune după direcțiile date de cei doi versori astfel: