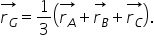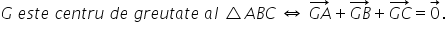Vectorul de poziție al centrului de greutate al unui triunghi

în această lecție o să discutăm

despre vectorul de poziție al Centrului

de greutate al unui triunghi începem

cu următoarea teoremă medianele

unui triunghi abc sunt concurente

într un punct numit centrul de

greutate al triunghiului care se

află pe fiecare mediană la două

treimi de vârf și o treime de bază

în triunghiul ABC am tot cu m n

și p mijloacele laturilor acestuia

iar cu g am punctul de intersecție

al medianelor punctul acesta G

se numește centrul de greutate

al triunghiului iar el este situat

pe fiecare mediană la două treimi

de vârf și o treime de bază prin

urmare lungimea segmentului AG

este două treimi din lungimea segmentului

a m iar g m este o treime din a

m Așadar a g supra cm este egal

cu 2 următoarea teoremă se referă

la vectorul de poziție al Centrului

de greutate al triunghiului are

loc această relație vectorul de

poziție al punctului G este 1 pe

3 din vectorul de poziție al punctului

a plus vectorul de poziție al punctului

b plus vectorul de poziție al punctului

C vomă lege în plan un punct o

și vom construi vectorii de poziție

ai punctelor a b c și g Iată o

a este vectorul de poziție al punctului

a o b este vectorul de poziție

al punctului b și așa mai departe

și acum Haideți să demonstrăm această

relație pornim de la această relație

a g supra g m este egal cu doi

și atunci vectorul de poziție al

punctului G se poate scrie astfel

egal cu vectorul de poziție al

punctului a plus doi ori vectorul

de poziție al lui m supra 1 plus

2 Și acum se exprima vectorul de

poziție al punctului m ținând cont

de faptul că M este mijlocul segmentului

BC prin urmare vectorul de poziție

al punctului m va fi semi suma

vectorilor de poziție a punctelor

b și c r b plus c supra 2 Și acum

înlocuim această expresie în relația

de mai sus din aceste două relații

obținem că vectorul de poziție

a punctului G este egal Cum vectorul

de poziție al punctului a plus

doi ori în loc de r m scrie în

formula de mai jos r b plus r c

supra 2 și totul supra 1 plus 2

3 aici se simplifică 2 și obținem

că vectorul de poziție a punctului

G la final cu r a plus b plus c

totul supra 3 așadar am demonstrat

această teoremă și în continuare

să vedem o proprietate a centrului

de greutate al triunghiului G este

centrul de greutate al triunghiului

Dacă și numai dacă suma vectorilor

g a g b și g c este egală cu vectorul

nul vom demonstra această proprietate

în ambele sensuri mai întâi implicația

directă presupunem că G este centrul

de greutate și trebuie să arătăm

că suma acestor vectori este egală

cu vectorul nul Așadar știind că

G este centrul de greutate prin

urmare Putem să scriem că vectorul

de poziție al punctului G este

1 pe 3 pe lângă a plus b plus RC

adică trei ori r g este egal cu

a plus b plus RC sau r a plus R

B plus r c minus 3 r g este egal

cu vectorul nul această relație

se mai poate scrie și astfel a

minus a r g plus r b minus r g

plus r c minus r g egal cu vectorul

nul Și acum dacă ne uităm pe figură

observăm că e r a minus r g este

egal cu vectorul a apoi r b minus

r g este egal cu vectorul DB iar

r c minus r g este egal cu vectorul

c c am obținut Așadar că suma acestor

vectori este egală cu vectorul

nul prin urmare am arătat că implicația

directă este adevărată și acum

să vedem și reciproc presupunem

că are loc această relație și trebuie

să demonstrăm că G este centrul

de greutate al triunghiului Adică

trebuie să demonstrăm că punctul

G este situat pe fiecare mediană

notăm cu M mijlocul lui bc n mijlocul

lui ac și p mijlocul lui AB observăm

că DB este suma vectorilor g a

m și m b apoi vectorul g c se poate

scrie ca suma vectorilor cm și

m c iar g a este g m plus ma acum

adunăm aceste trei relații membru

cu membru și obținem că g a plus

GB plus Jessie este egal cu 3 ori

m plus MB plus Mc plus ma știm

din ipoteză că această sumă este

egală cu vectorul nul apoi din

moment ce punctul m este mijlocul

segmentului BC înseamnă că vectorii

MB și MC sunt vectori opuși prin

urmare suma acestor doi vectori

va fi egală cu vectorul nul această

sumă este egală cu vectorul nul

din ipoteză și atunci avem trei

GM plus m am este egal cu vectorul

nul sau 3 g m este egal cu minus

ma dar opusul vectorului m a este

vectorul a m din moment ce am ajuns

la această relație 3G m este egal

cu a m înseamnă că vectorii g m

și a m sunt vectori coliniari Așadar

punctul G aparține segmentului

a m am arătat astfel că punctul

C este situat pe mediana a m în

mod Analog se arată că punctul

C este situat pe mediana b n și

g aparține și segmentului c p așa

dar am arătat că punctul G este

centrul de greutate al triunghiului

el fiind punctul de intersecție

al medianelor