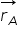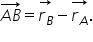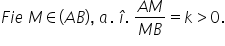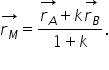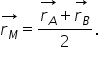Vectorul de poziție al unui punct (aplicații)
Tag-uri
Partajeaza in Google Classroom
Transcript
avem următoarea problemă Fie a
b c d un trapez iar m n linie mijlocie
se cere se exprimă în vectorul
de poziție al mijlocului segmentului
MN în funcție de vectorii de poziție
ai punctelor a b c și d am notat
cu p mijlocul segmentului MN și
trebuie să exprime în vectorul
de poziție al punctului pe Haide
să ne reamintim formula vectorului
de poziție al unui punct M ce împarte
un segment AB în raportul k Acesta
are următoarea formulă a plus k
r b supra 1 plus k iar în cazul
în care m este mijlocul segmentului
AB atunci vectorul de poziție a
punctului m va fi egal cu vectorul
de poziție a punctului a plus vectorul
de poziție a punctului b supra
2 din moment ce p este mijlocul
segmentului MN vom aplica această
formulă prin urmare vectorul de
poziție al punctului p va fi egal
cu vectorul de poziție al punctului
m plus vectorul de poziție al punctului
n supra 2 care se mai poate scrie
1 pe 2 pe lângă a r m plus r n
și acum se exprimă în vectorii
de poziție ai punctelor m și n
în funcție de vectorii de poziție
ai punctelor a b respectiv c d
m este mijlocul segmentului AB
atunci m va fi egal cu vectorul
de poziție al punctului a lui de
poziție al punctului b totul supra
2 iar vectorul de poziție a punctului
n va fi egal cu vectorul de poziție
al punctului D plus vectorul de
poziție al punctului C totul supra
2 din aceste relații obținem următoarea
relație vectorul de poziție al
punctului p este egal cu 1 pe 2
pe lângă în loc de RM vom avea
r a plus R B supra 2 plus în loc
de r&m scrie această relație RD
plus irc supra 2 egal cu 1 supra
4 pe lângă a plus R B plus RCF
plus RDS am reușit Așadar să exprimăm
vectorul de poziție a punctului
p în funcție de vectorii de poziție
ai punctelor a b c și d și mai
facem o problemă Fie abc un triunghi
M un punct situat pe latura ab
în punctul n pe latura AC astfel
încât a m supra MB este egal cu
1 pe 2 iar a n supra n egal cu
2 pe 3 exprimați vectorii de poziție
ai punctelor m și n avem Așadar
un punct M situat pe latura ab
astfel încât a m supra MB să fie
egal cu k și egal cu 1 pe 2 o să
folosim Așadar prima formulă în
care o să îl Înlocuim pe capacul
1 pe 2 prin urmare în vectorul
de poziție al punctului m va fi
egal cu vectorul de poziție al
punctului a plus 1 pe 2 ori vectorul
de poziție al punctului b supra
1 plus 1 pe 2 egal cu vectorul
de poziție al punctului a plus
1 pe 2 ori vectorul de poziție
al punctului b totul supra 3 pe
2 egal mă îmi scrii această fracție
ca o sumă de două fracții avem
vectorul de poziție al punctului
a supra 3 pe 2 plus cea de a doua
fracție este 1 pe 2 ori vectorul
de poziție a punctului b supra
3 pe 2 egal în continuare cu 2
pe 3 ori vectorul de poziție al
punctului a plus iar aici o să
avem 1 pe 2 ori 2 pe 3 se simplifică
2 și rămâne 1 pe 3 așa dar aici
o să avem 1 pe 3 ori vectorul de
poziție a punctului b a scris Așadar
vectorul de poziție al punctului
m în funcție de vectorii de poziție
ai punctelor a și b și acum să
scriem vectorul de poziție al punctului
n avem Raportul a n supra m c egal
cu 2 pe 3 prin urmare k va fi 2
supra 3 n aparține segmentului
ac astfel încât a n supra m c egal
cu k și egal cu 2 pe 3 atunci vectorul
de poziție al punctului n va fi
egal cu vectorul de poziție al
punctului a plus în această formulă
o să înlocuim pe k cu 2 supra 3
și avem 2 pe 3 înmulțit cu vectorul
de poziție a punctului C supra
1 plus 2 pe 3 egal cu a plus 2
supra 3 r c supra 5 pe 3 nu scrie
iarăși ca o sumă de două fracții
ai se inversează fracția de la
numitor o să avem 3 supra 5 ori
vectorul de poziție al punctului
a plus iar aici o să avem 2 pe
3 ori 3 pe 5 se simplifică 3 și
ne rămâne în doi pe cinci așa dar
o să scriem 2 supra 5 înmulțit
cu vectorul de poziție al punctului
c am reușit astfel să scriem și
vectorul de poziție a punctului
n în funcție de vectorii de poziție
a punctelor a și c
Vectorul de poziție al unui punct Ascunde teorie X
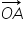se numește vector de poziție al punctului A.
Navigare în lectii
Cumpara abonament
