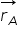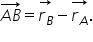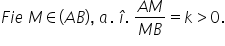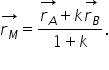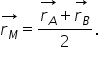Vectorul de poziție al unui punct (teorie)
Tag-uri
Partajeaza in Google Classroom
Transcript
în această lecție discutăm despre
vectorul de poziție al unui punct
dacă avem în plan un punct om și
un alt punct A atunci vectorul
având originea în punctul o și
extremitatea în punctul a se numește
Vector de poziție al punctului
a sau Vector legat de punctul O
sau de Polul om acesta se notează
cu r indice am Să considerăm acum
un alt punct b în plan și să încercăm
să exprimăm vectorul ab cu ajutorul
vectorilor de poziție a punctelor
a și b vectorul de poziție al punctului
b va fi o b iar acesta se notează
cu r indice b observăm Așadar că
vectorul ab este diferența dintre
vectorii o b și o a cu alte cuvinte
vectorul AB este egal cu vectorul
de poziție al punctului b minus
vectorul de poziție al punctului
a am găsit Așadar o exprimare a
vectorului ab în funcție de vectorii
de poziție ai punctelor a și b
ne propunem în continuare să găsim
o exprimare a vectorului de poziție
al unui punct M care împarte un
segment AB între un raport dat
avem Așadar un punct M care aparține
segmentului AB și ne propunem să
găsim o expresie a vectorului de
poziție al punctului m care împarte
segmentul ab în raportul a m supra
MB egal cu k unde k este un număr
pozitiv să desenăm Așadar un segment
AB și avem un punct oarecare m
fixăm în plan un punct om iar om
va fi vectorul de poziție al punctului
m indice m ne propunem să scriem
acest Vector RM în funcție de vectorii
de poziție ai punctelor a și b
acesta este vectorul de poziție
al punctului a iar o b este vectorul
de poziție al punctului b Dacă
M este situat în interiorul segmentului
AB înseamnă că punctele a m și
b sunt coliniare și de asemenea
vectorii a m și m b sunt coliniari
prin urmare Putem să scriem următoarea
relație vectorială a m este egal
cu k ori m b dar a m se poate scrie
în funcție de vectorii de poziție
ai punctelor a și m astfel indice
m minus a r n e c a este egal cu
k pe lângă vectorul MB se poate
scrie a r b minus a r m acum o
să desfacem aici paranteza vectorul
de poziție al punctului m minus
vectorul de poziție al punctului
a este egal cu k înmulțit cu vectorul
de poziție al punctului b minus
k ori vectorul de poziție al punctului
m r m plus k ori r m este egal
cu a plus k ori verbe aici putem
se dă factor comun pe r m și avem
r m pe lângă 1 plus k este egal
cu a plus ca apa ori rb din această
relație putem să exprimăm vectorul
de poziție al punctului m RM va
fi egal cu a plus ca apa ori rb
supra 1 plus k am găsit Așadar
o expresie a vectorului de poziție
al unui punct M care împarte un
segment AB într un rapport dat
k în cazul în care k este egal
cu 1 atunci punctul M va fi mijlocul
segmentului AB să vedem ce expresivă
a avea vectorul de poziție al punctului
m în cazul în care m este mijlocul
segmentului așa dar în cazul în
care k este egal cu 1 atunci punctul
m este mijlocul segmentului AB
iar vectorul de poziție al punctului
m se va scrie a astfel avem r a
plus Urban în această formulă Înlocuim
pe capacul 1 totul supra 2 să reținem
Așadar și această relație ce exprimă
vectorul D poziție al unui punct
m în cazul în care m este mijlocul
segmentului AB
Vectorul de poziție al unui punctAscunde teorie X
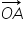se numește vector de poziție al punctului A.
Navigare în lectii
Cumpara abonament
