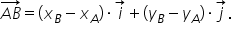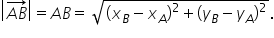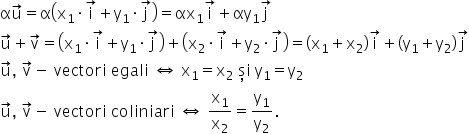Descompunerea unui vector într-un reper cartezian
Tag-uri
Partajeaza in Google Classroom

Transcript
avem un sistem de axe x o y în
care vom reprezenta doi vectori
ce vor indica sensul pozitiv pentru
fiecare axă acești doi vectori
vor avea modulul egal cu unitatea
și ei se vor numi versuri voi nota
cu verisorul Axa o x și cu j versorul
axa o y A dar modulul vectorului
e este egal cu modulul vectorului
J și este egal cu 1 Să considerăm
acum un punct A iar un endo regione
a sistemului de axe cu acest punct
se obține un Vector numit vectorul
de poziție al punctului a în continuare
ne propunem să scriem acest Vector
o a în funcție de versorii i și
j cu alte cuvinte spunem că am
descompus vectorul o a după direcțiile
versorilor i și j descompunerea
unui Vector este operația inversă
adunării prin urmare vom folosi
regula paralelogramului și vom
duce din a paralele la cele două
axe vointa sis.com a unu Iar acest
punct cu ei doi voi nota abscisa
punctului a cu X indice a și ordonata
punctului a cu y indice a de asemenea
voi construi și vectorii o a 1
respectiv o a 2 Aplicând regula
paralelogramului observăm că vectorul
o a este suma vectorilor o a 1
și o a 2 dar vectorul o a 1 și
versorul e sunt vectori coliniari
prin urmare vectorul o a 1 se obține
Înmulțind versorul e cu un scalar
cu o constantă iar această constantă
este chiar abscisa punctului a
pe care am notată cu X indice a
De exemplu dacă x indice a este
5 atunci vectorul o a 1 este egal
cu 5 ori e pentru că e are lungimea
egală cu unitatea Așadar vectorul
o a 1 se scrie cu ajutorul versorul
lui e astfel x indice a ori i iar
vectorul o a 2 va fi y la fel Aceștia
sunt vectori coliniari iar y a
este constanta cu care trebuie
să înmulțim versorul j pentru a
obține vectorul o a doi am reușit
astfel să scrie în vectorul de
poziție al punctului a cu ajutorul
versorilor e și j sau mai putem
spune că am descompus vectorul
o a după direcțiile versorilor
i și j numerele x și y a se numesc
coordonatele vectorului o a acestea
erau și coordonatele punctului
a această expresie pe care am obținut
o Aici se numește expresia analitică
a vectorului o Să considerăm acum
un alt punct b ducem vectorul de
poziție al punctului b ne propunem
să exprimăm în continuare vectorul
OB în funcție de versuri I și j
pentru aceasta duce în paralele
la cele două axe de coordonate
lupte acest punct cu B1 iar abscisa
punctului b o notez cu X indice
b era acest punct o să notezi cu
B2 iar ordonata punctului b cu
y de de asemenea construim și vectorii
ob1 acesta cu galben respectiv
ob 2 și observăm Așadar că vectorul
OB se poate scrie ca suma vectorilor
ob1 și ob 2 vectorul o b 1 și versorul
e sunt vectori coliniari prin urmare
ob1 se poate scrie cu ajutorul
verișorul lui a astfel x indice
b ori e iar ob2 este yba-11 vectorul
OB după direcțiile versurilor i
și j coordonatele punctului b sunt
x indice b și y indice b iar acestea
vor fi și coordonatele vectorului
de poziție o b și acum Haideți
să construim și vectorul ab și
să exprimăm acest Vector în funcție
de versorii i și j observăm că
vectorul ab este egal cu o b minus
o a vrea mintesc că la diferență
vectorilor săgeata Indică descăzutul
Deci avem o b minus a o a și acum
înlocuim vectorii o b și o a cu
expresiile analitice găsite mai
sus în loc de o b o să avem x b
ori y plus y b ori Z minus x a
n i plus y ori Z desfacem paranteza
și aranjăm termenii avem x b o
e minus x a ori y plus y b o j
minus y a ori j din primii doi
termeni de factor comun pe și avem
x b minus x a înmulțit cu e plus
y b minus y a înmulțit cu j așa
dar aceasta este expresia analitică
a vectorului ab în funcție de versuri
I și j sau cu alte cuvinte descompunerea
vectorului ab după direcțiile versorilor
i și j aceste numere din fața versorilor
se numesc coordonatele vectorului
Deci coordonatele vectorului a
b sunt x b minus x a respectiv
y b minus y a în continuare ne
propunem să găsim o formulă de
calcul pentru lungimea vectorului
ab pentru aceasta vom construi
un triunghi dreptunghic și vom
aplica teorema lui Pitagora în
acest triunghi dreptunghic acest
segment are lungimea egală cu x
b minus x a Iar acest segment are
lungimea egală cu y că lungimea
vectorului AB este radical din
x b minus x a la pătrat plus y
b minus y a la pătrat să reținem
Așadar aceste două formule descompunerea
vectorului ab după direcțiile versurilor
e și j respectiv formula de calcul
pentru lungimea vectorului ab în
continuare aș vrea să mai facem
câteva observații dar să avem un
Vector un care are următoarea expresie
analitică X1 ori y plus y 1 ori
j și un alt Vector v care are expresia
analitică X2 plus y 2 ori j atunci
definim produsul dintre vectorul
u și scalarul Alfa astfel Alfa
ori este egal cu alfa pe lângă
x 1 y plus y 1 ori j desfacem paranteza
și obținem Alpha x 1 x plus Alpha
y1 origi suma dintre vectorii u
și v se va face pe componente se
adună coordonatele celor doi vectori
avem x 1 plus x 2 ori y plus y
1 plus y 2 ori j în mod Analog
definit și scăderea vectorilor
u și v condiția ca vectorii u și
v să fie egal este ca x-1 să fie
egal cu x 2 și 1 să fie egal cu
y 2 așa Dar cei doi vectori trebuie
să aibă aceleași coordonate iar
doi vectori ușii V sunt coliniari
Dacă și numai dacă are loc această
relație x 1 supra X2 egal cu 1
supra y 2 cu alte cuvinte doi vectori
sunt coliniari dacă au coordonatele
proporționale în clipul următor
o să facem câteva exerciții pentru
a înțelege mai bine aceste operații
cu vectori

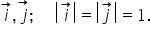
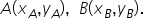
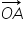 se descompune după direcțiile date de cei doi versori astfel:
se descompune după direcțiile date de cei doi versori astfel: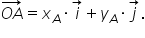
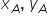 se numesc coordonatele carteziene ale punctului A sau coordonatele vectorului
se numesc coordonatele carteziene ale punctului A sau coordonatele vectorului 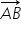 se descompune după direcțiile date de cei doi versori astfel:
se descompune după direcțiile date de cei doi versori astfel: