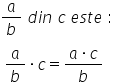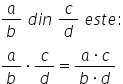Aflarea unei fracții dintr-un număr natural sau dintr-o fracție

să aflăm acum o fracție dintre

un număr și avem acest exemplu

Un ciclist vrea să parcurgă un

drum cu lungimea de 30 de km el

parcurge trei cincimi din drum

Câți kilometri a parcurs pe această

problemă o putem rezolva și folosind

un de segmente astfel știind că

avem un drum cu lungimea de 30

de km Moon de ceai de Să considerăm

că acest segment reprezintă Drumul

care are o lungime de notăm sus

30 de kilometri bun ciclistul parcurge

trei cincimi din drum și vrem să

vedem Câți kilometri a parcurs

eu de fapt Păi dacă el parcurge

trei cincimi din drum Ce trebuie

să facem cu acest întreg trebuie

să îl împărțim în cinci părți egale

și avem așa aparte încă una avem

trei părți 450 unu doi trei patru

cinci părți egale ciclistul parcurge

trei cincimi din drum de cel parcul

c35e venim aici și notăm trei cincimi

de și 3 supra 5 din lungimea drumului

adică din 30 de km bun și noi trebuie

Acum să vedem Câți kilometri reprezintă

această distanță trei cincimi din

30 putem să ne gândim și în felul

următor Cât reprezintă o parte

pe o parte este de fapt o cincime

Deci 1 supra 5 din 30 de km acum

dacă toată lungimea drumului este

de 30 de km noi avem cinci părți

egale cât are fiecare parte foarte

simplu facem 30 împărțit la 5 obținem

șase kilometri Deci o cincime din

30 de km adică acest segment fiecare

segment în parte reprezintă câte

6 km ciclistul nostru a parcurs

trei cincimi Păi asta înseamnă

că trebuie să înmulțim pe trei

pentru că avem trei asemenea părți

cu 6 deci 3 înmulțit cu 6 obținem

18 km Deci venim aici notăm că

trei cincimi din 30 se prezintă

18 km cum ținem acum răspunsul

fără a face aceste calcule separat

Păi o cincime din 30 de kilometri

putem să transcriem în limbaj matematic

astfel cuvântul din se traduce

prin operația de înmulțire Deci

avem cum supra 5 înmulțit cu 30

și acuma întotdeauna un număr natural

poate fi scris ca o fracție De

ce putem face acest lucru intotdeauna

putem să trecem numărul natural

respectiv supra 1 trecem numitorul

unu pentru că linia de fracție

reprezintă operația de împărțire

și 30 împărțit la 1 ne dă 30 Acum

trebuie să vedem cum înmulțim două

fracții e foarte ușor să reținem

regula Haideți să scriem egalul

în dreptul liniilor de fracție

vom înmulțit numărătorii între

ei și numitorii între ei și vom

avea așa linia de fracție la numărător

130 iar la numitor 5 ori unu și

vom obține 30 cinci ore unu cinci

și cât ne dă obținem 6 Iată avem

aici 6 km aceeași regulă o putem

aplica și în această situație trei

cincimi din 30 traducem matematică

avem aici operația de înmulțire

3 supra 5 înmulțit cu 30 Pe care

cum îmi scrie răstimp tot sub formă

de fracție și întotdeauna trecem

numitorul unu este egal mai departe

cu înmulțim Haideți Să arătăm din

nou numărători între ei și numitorii

între ei Deci vom avea trei ori

30 supra 5 ori și obținem 90 supra

5 Dacă împărțim 90 la 5 obținem

18 băiat exact ce am avut șapte

și trei cincimi din 30 reprezintă

este egal cu numărul 18 și putem

face calculul exact cum am arătat

aici alt exemplu să Reprezentăm

printr un desen și să calculăm

două treimi din cinci din nou Vrem

să aflăm o fracție dintre un număr

natural Cum putem să Reprezentăm

printr un desen precum avem aici

numărul 5 acest număr reprezintă

de fapt în numărul de întregi Deci

vom avea nevoie de 5 întregi identici

și ia tăi deja am desenat aici

avem 1 2 3 4 5 noi vrem Acum să

vedem cât reprezintă două treimi

din acești 5 întregi însă mai înainte

Ce avem de făcut Vrem să vedem

cât reprezintă sau cum exprima

pentru un desen două treimi dintre

un singur întreg Deci venim aici

și vom nota vom împărți acest întreg

în trei părți egale și vom hașura

două părți pentru că pe noi ne

interesează două treimi din acest

întreg la fel procedăm și cu ceilalți

intregi și iată am obținut acest

desen a ce am reprezentat aici

reprezintă două treimi din 560

să vedem ce fracție obține pe care

este numitorul fracției obținute

Păi avem cinci întregi identici

fiecare este împărțit în trei părți

egale acum ce exprimă numitorul

numitorul exprimă numărul de părți

în care am împărțit întregul Păi

și noi avem fiecare întreg împărțit

în una două trei părți Deci numitorul

este 3 numărătorul ne arată câte

părți Considerăm Păi și avem una

două trei patru cinci 6 7 8 9 10

Deci numărătorul este egal cu 10

2 pe 3 din 5 este egal cu 10 supra

3 ca mai facem acest calcul traducem

cuvântul din prin operația de înmulțire

și avem 2 supra 3 înmulțit cu 5

pe care îl scriem Cum să scriem

sub formă de fracție 5 supra unu

și acum înmulțim aceste două fracții

trecem linia de fracție și înmulțim

numărătorii între ei Deci 2 ori

5 și numitori între a 3 ori 1 și

vom avea 2 ori 5 10 3 ori 1 3 10

supra 3-a extract ce am avut aici

Dacă făceam parte calcul de exemplu

calculam două treimi de două 2

supra 3 din nu din 5 din 6 pe procedăm

la fel folosind direct această

regulă cuvântul din se traduce

matematică prin operația de înmulțire

De ce avem 2 supra 3 înmulțit cu

6 supra 1 și vom avea linie de

fracție înmulțim numărătorii între

ei Deci 2 ori 6 supra 3 ori 1 și

vom obține 12 supra 3 Putem să

simplificăm prin trei sau putem

să facem împărțirea direct 12 împărțit

la 3 ne dă patru sau putem să notăm

idee să scriem așa timp să ne uităm

că avem patru supra 1 dacă simplificăm

prin trei deci Rezultatul este

4 Haideți acum să vedem cum procedăm

când Vrem să aflăm o fracție din

alta fracție din o să Reprezentăm

printr un destin și să calculăm

acum două treimi dintre alte fracții

și anume din 5 supra 9 Păi mai

întâi avem nevoie de ce anume Vrem

un întreg și în acel întreg să

Reprezentăm fracția 5 supra 9 Deci

am notat aici întregul pe care

deja îl am în părți în nouă părți

egale Una două trei patru cinci

șase șapte opt și nouă acum vom

alege cinci din acest text nouă

părți cid sau alegem pe aceasta

pe aceasta alegem cinci părți Deci

una două trei patru cinci munți

acum ce am reprezentat aici reprezintă

fracția este fracția 5 supra 9

și acesta este noul întreg și noi

trebuie să Reprezentăm acum două

treimi din acest întreg Păi pentru

aceasta vom împărți acest întreg

să îi spunem în trei părți egale

pentru că vrem să Reprezentăm fracția

2 supra 3 Deci vom avea aici o

parte mai fur la aceasta și aici

le vom obține pe următoarele două

Deci avem o parte două trei părți

egale și selectăm alegem Considerăm

două din aceste trei părți și să

alegem pe această parte Deci una

și încă una și pe aceasta ce am

notat aici cu albastru reprezintă

două treimi din din 5 supra 9 Păi

cât vom obține Cu cât este egal

mai ai nevoie momentan să facem

un calcul putem să ne uităm direct

pe desen Pentru a stabili rezultatul

Haideți să împărțim tot întregul

în așa fel încât să avem doar părți

egale Deci trebuie să completăm

aici desenul și voi completa astfel

și atât tot ce am obținut sunt

părți egale această parte egală

cu aceasta cu aceasta și cu acestea

hașurate aici câte părți avem în

total cu alte cuvinte care este

numitorul reprezentat numitorul

fracției care e reprezentată prin

acest destin Păi avem una două

trei patru cinci șase șapte opt

nouă părți cu încă 918 cu încă

927 asta înseamnă că numitorul

este 27 câte părți Considerăm pe

ele în considerați aceastea care

sunt hașurate știi cu galben și

cu albastru avem 1 2 3 4 5 cu încă

5 înseamnă că avem 10 părți considerate

De ce obținem fracția 10 supra

27 pe același lucru obțineam și

dacă scriam astfel cuvântul din

Satra ce matematică prin operația

de înmulțire avem 2 supra 3 înmulțit

cu 5 supra 9 și vom avea înmulțim

numărătorii între ei Deci 2 ori

5 supra 3 ori 9 3 înmulțit cu 9

și vom obține 10 supra 3 ori 9

27 iar exact ce am obținut și aici

Haideți să mai facem și alte exemple

să calculăm de exemplu 7 supra

5 din 2 supra 11 pe ce vom obține

din nou vom avea 7 supra 5 cuvântul

din Tinca operație de înmulțire

ori 2 pe 11 și acum trecem in ea

de fracție la numărător înmulțim

nu acești doi numărători 7 ori

2 și la numitor obținem 5 ori 11

și rezultatul este 14 supra 55

încă un exemplu trei pătrimi Deci

3 supra 4 din 8 pe 5 si vom obține

3 supra 4 cuvântul din înscriem

ca o operație de înmulțire Deci

ori 8 supra 5 și acum înmulțim

3 ori 8 iar la numitor vom obține

patru ori 5 ori 3 ori 8 ne dă 24

4 8 5 ne dă 20 putem să simplificăm

aici prin Cât prin 4 și vom avea

așa 24 împărțit la 4 ne dă 620

împărțit la 4 ne dă 50 am obținut

șase pe cinci fracții ireductibilă

ca și aceasta de mai sus cu alte

cuvinte casă concluziona atunci

când Vrem să aflăm o fracție de

exemplu a supra b dintru un număr

de din ce cum vom proceda Păi vom

avea a supra b înmulțit cu c iar

pe ce acest număr natural înscriem

supra 1 si supra 1 și vom obține

la numărător a orice iar la numitor

ban muncit cu unu adică b dacă

Vrem să aflăm o fracție dintr o

altă fracție de exemplu din c supra

de aici aveam în situația particulară

în care D era egal cu 1 d c d este

un număr natural din fi Dent nenul

ca și b Toma avea a supra b înmulțit

cu c supra D Deci vom obține înmulțim

numărătorii între a a orice și

numitori între ei D în cu d acestea

sunt cele două reguli prin care

aflăm o fracție dintre un număr

natural sau dintre o altă fracție