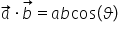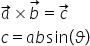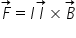Câmpul magnetic. Produsele vectorilor. Forţa electromagnetică.

în cea de a unsprezecea lecții

despre curentul electric continuu

vom discuta despre câmpul magnetic

despre produsele vectorilor și

despre forța electromagnetică câmpul

magnetic se manifestă în experimentele

cele mai simple prin magneți permanenți

dar și în jurul curenților electrici

experimental se observă efectul

Câmpului magnetic din jurul acestor

două tipuri de dispozitive prin

folosirea așa numitului AC magnetic

sau prin folosirea piliturii de

fier sau pulberi de fier acul magnetic

este un magnet permanent cu greutate

foarte mică foarte ușor uzuali

last întâlnit în busole pentru

a indica nordul și sudul magnetic

al pământului când pământul are

un câmp magnetic foarte slab cu

care un magnet permanent Care este

acest AC magnetic va interacționa

și în felul acesta vârful ce corespunde

polului Nord al magnetului se va

alinia cu Polul Nord al pământului

la fel vârful ce corespunde Polul

Sud al magnetului se va alinia

cu Polul Sud al pământului și în

felul acesta busola arată alinierea

cu polii magnetice Pământului în

locația respectivă de a doua metodă

de a de a folosi câmpul magnetic

în experimente și de al vizualiza

este pilitura de fier să dăm mânca

exemplu acest magnet permanent

de gene această imagine vedeți

un magnet permanent În care din

nou Polul Nord al magnetului este

colorat în roșu și Polul Sud este

colorat în albastru această convenție

Generală de culoare pentru polii

unui magnet permanent liniile de

câmp ale unui astfel de magnet

ies din Polul Nord și intră prin

Polul Sud avem câmpuri sau linii

de câmp magnetic cu forma în general

echivalentă cu cea a doua sarcini

electrice opuse vă reamintesc că

am studiat liniile de câmp electrice

în lecții precedent putem studia

în mod practic forma acestora linii

de câmp dacă folosim pilitura de

fier tot ce vedeți dumneavoastră

ca linii foarte faină Aici este

pilitura de fier sau pulbere foarte

ușoare de fier care prin interacțiunea

cu câmpul magnetic al magnetului

se aliniază pe liniile de câmp

sau liniile de forță ale Câmpului

magnetic și în acest fel putem

să le vizualizez în mod direct

De asemeni în această imagine se

arată o serie de șapte compase

sau busole foarte mici în așa fel

încât putem din nou vizualiza tangenta

la linia de câmp în fiecare punct

de ce vedem Spre exemplu aici că

nordul compasului este orientat

așa și sudul compasului în sus

Deci în punct pe linia de câmp

tangenta la linia de câmp este

arătată de către o busolă de către

acului busolei și apoi vedem cum

se schimbă tangenta la linia de

câmp Pe măsură ce ne mișcăm aproximativ

pe aceeași linie de câmp între

Polul Nord și Polul Sud Deci folosind

o combinație de ac magnetic și

pilitura de fier putem vedea această

formă a liniilor de câmp magnetice

după cum am vorbit în afară de

un magnet permanent putem folosi

ca sursă pentru un câmp magnetic

și un curent electric pentru că

se stabilește experimental că orice

curent electric atât continuu cât

și alternativ sau de altă dependență

temporală Zici orice curent magnetic

generează în jurul său un câmp

orice cântă electric generează

în jurul său un câmp magnetic putem

vedea am aceasta experimental cu

un dispozitiv de felul următor

Deci foarte simplu ce vedeți aici

este un fir conductor prin care

trece un curent electric de ce

El este conectat la o sursă care

nu se vede nimeni Și în jurul lui

am împrăștiat din nou pilitura

de fier după cum se vede mp3 de

fier interacționează cu un câmp

Care este invizibil bineînțeles

dar această distribuție foarte

simetrică a piliturii de fier arată

că există o interacțiune puternică

ce se manifesta asupra ei și formele

acestui câmp sunt concentrice sunt

circulare și concentrice în jurul

firului străbătut de curent electric

Deci înjur unui conductor liniar

liniile de câmp magnetic generat

sunt circulare iar sensul lor este

dat de așa numita regula burghiului

Deci pentru a înțelege această

regulă a burghiului Care este următoarea

de întâi Să formulăm și apoi să

vorbim despre ea Deci avem un burghiu

pe care foarte Generic îl desenez

așa și vă puteți imagina foarte

ușor că dacă burghiul este rotit

în această direcție el va înainta

Pe de altă parte dacă el este rotit

în direcția opusă el se va retrage

din prune virtual material în care

el este în care ele se află introdus

burghiului mai poate fi numită

și regula șurubului să zicem și

dacă aveți oarecare probleme să

vă imaginați legătura dintre sensul

de rotație și sensul de înaintare

al unui burghiu sau unui șurub

Vă rog frumos să faceți această

mică experiență dumneavoastră luați

un șurub o șurubelniță și pur și

simplu înșurubat șurubul pentru

material și observați și rețineți

conexiunea saule dintre sensul

în care învârtit pentru a produce

o înaintare și sensul în care învârtit

pentru a produce o retragere a

șuruburi în veci în cazul acesta

dacă curentul prin prin conductor

are sensul în sus vă dați seama

că trebuie să rotiți în acest sens

pentru Deci în sensul spre dreapta

burghiul pentru a înainta dacă

ar avea curentul dacă ar fi cu

sensul în jos atunci ar trebui

să rotiți burghiul spre stânga

pentru a obține acest sens sens

în jos acesta este regula burghiului

care Stabilește legătura dintre

sensul curentului electric și sensul

liniilor de câmp magnetic din jurul

lui o altă aplicație simplă a tu

lui magnet Câmpului magnetic generat

de un curent electric este solenoidul

solenoidul este un conductor în

formă de spirală cu rază constant

Deci exact acest conductor care

vedeți aici care nu este o serie

de cercuri și cercuri legate între

ele așa cum se vede ușor prin această

suprafață Care este transparentă

Deci tot Acest conductor este unul

singur un conductor continuu spiralele

aceluiași conductor în acest caz

liniile de câmp se pot vedea din

nou foarte ușor cu pilitura de

fier ele sunt paralele și echidistante

Deci un câmp uniform magnetic în

interiorul solenoidului și apoi

au forma foarte similară în exterior

cu cea a unui magnet permanent

cel de aici Sunt liniilor de câmp

se stabilește tot cu regula burghiului

de sol presupunem că curentul electric

care acest sens prin conductor

și atunci Puneți un burghiu imaginar

bineînțeles cu axul Da lungul axului

solenoidului și învârtit burghiul

în sensul curentului pe care îl

am are în cazul acesta în sus și

trebuie să Stabiliți În ce direcție

se va duce burghiul înainte sau

înapoi Bineînțeles că pentru acest

sens al curentului se va duce înainte

să discutăm despre produsele vectorilor

ele sunt de două tipuri produsul

scalar dintre doi vectori a și

b este definit ca a or b ori cosinus

de unghiul ta care este unghiul

dintre ei dintre cei doi vectori

Deci dacă aceasta este schema avem

vectorul a vectorul b și unghiul

tăiată dintre ei dintre cei doi

vectori atunci a ori b produs scalar

a doi vectori va fi modul lui a

modulul b înmulțit cu cosinus de

tata felul în care poate fi explicat

în continuare pentru mai multe

caritate acest produs este observând

Spre exemplu că a cosinus de teta

este proiecția vectorului a b vectorul

b Deci acest produs mai poate fi

scris ca a b ori b sau la fel dacă

proiectăm b vectorul de pe vectorul

a și notăm proiecția lui ca Da

adică proiecția lui d pe vectorul

a este egal cu a ori b a proprietățile

acestui produs în foarte simple

în primul rând se numește produs

scalar pentru că deși și a și b

sunt vectori produsul scalar un

scalar nu în Vector despre scalar

și vectori am discutat în prima

lecție de cinematică vă rog să

revizuiți diferența dintre Scala

și Vector din acea lecție O primă

proprietate este că dacă a e paralel

cu b atunci produsul a ori b este

egal cu produsul modulelor a și

b pentru că cosinus de tata este

1 cosinus de 0 este 1 paralele

înseamnă teta egal cu 0 Deci cosinus

de 0 care 1 putem avea tot Semnul

plus și semnul minus depinzând

de Cum anume sunt paralel CD Vector

pot să fie paralel cu același sens

caz în care obține Semnul plus

sau paralel cu semn opus cazul

în care produsul are semnul minus

dacă ei sunt perpendiculari atunci

produsul celor doi vectori este

nul este 0 pentru că perpendiculare

înseamnă cosinus de 90 de grade

Care este 0 Deci produsul scalar

a doi vectori perpendiculari este

0 și de asemeni putea observa că

a orbi este egal cu b ora aceasta

se poate observa și Deci un al

doilea tip de produs între doi

vectori este așa numitul produs

vectorial care are această notație

fi definit ca a orbi ore un versor

n pe care o voi explica imediat

ori sinusul unghiului dintre a

și b Deci avem vectorul A vectorul

B unghiul teta dintre ele și atunci

a ori b este un Vector Care este

de a lungul versului An are versul

n este perpendicular pe planul

format de cinci doi vectori originali

Deci dacă luăm planul dintre cei

doi vectori pe care o vezi acum

Deci suprafața hașurată este planul

format de vectorii a și b n este

versul adică vechi dorul de modul

1 perpendicular pe c Pe planul

celor doi vectori b vectorial va

avea modul a b sinus Deta și direcția

Da lungului an trebuie să mai stabilim

numai sensul la după ce am stabilit

modulul și direcția trebuie să

stabilim sensul adică este în sus

pe această direcție sau în jos

Aceasta este întrebarea în legătură

cu sensul produsului vectorial

și pentru aceasta folosim așa numita

regula burghiului pe care îmi explica

tu din nou punem un burghiu de

ce avem un burghiu pe care îl desenez

eu simplu aici dar lungul direcției

m și îl rotim astfel încât să învârtim

a peste b Deci sensul a aur b nu

este egal cu b ora de vom vedea

imediat Care e legătura Deci îl

învârtim pe primul Vector peste

al doilea factor 12-a peste b Deci

sensul de rotație a burghiului

va fi așa pentru a roti pe ape

este b și atunci trebuie să stabilim

În ce sens înaintează sau se retrage

burghiul acestor în cazul acestei

rotiri burghiul va înainta Deci

acesta este sensul produsului Tăria

se mai folosește și așa numita

regulă a mâinii stângi ca variantă

pentru regula burghiului dar ea

este mai ușor de folosit numai

în cazul particular în care a și

b sunt perpendiculare Deci imaginații

vă dacă ar fi perpendicular pe

b d c avem această situație a e

în aceeași poziție b e este perpendicular

pe a form în de aici de 90 de grade

și Ce trebuie să faceți dumneavoastră

trebuie să puneți mâna stângă cu

degetele cele patru degete de a

lungul lui a și a astfel încât

b să intre în palmă în acest caz

înseamnă că palma dumneavoastră

va fi de a lungul ecranului sau

pe ecran atunci degetul mare îndreptat

în sus vă va arăta sensului a or

b Deci aur b va fi în sus și perpendicular

pe planul format de B ora el Alegeți

dumneavoastră ce regulă folosiți

eu praf personal Prefer regula

burghiului pentru că e mai general

proprietățile sunt simple dacă

a este paralel cu b atunci unghiul

este 0 sau 180 de grade depinzând

de orientarea lor relativă de ce

este 0 sau 180 dar sinus de 0 și

sinus de 180 sunt amândouă 0 Deci

în cazul vectorilor paralele atât

cu același sens cât și cu sensuri

contrare produsul vectorial este

nu este 0 în cazul vectorilor perpendiculari

teta este 90 de grade și atunci

deoarece stii de 90 de grade este

unul aur b este egal cu a are modulul

a b și orientat da lungului De

asemeni se poate vedea foarte ușor

că aur b este egal cu minus b ori

A deci în cazul lui Berea trebuie

să rotim b peste ei și în acel

caz trebuie să rotim burghiul în

sens invers pentru ARO tip de pe

stea în acel caz burghiul se va

retrage de sensul va fi celălalt

forța electromagnetică De ce am

discutat despre faptul că un magnet

permanent are un câmp magnetic

în jurul lui și un curent electric

are un câmp magnetic în jurul lui

rezultă de aici că e normal să

existe o forță între un câmp magnetic

și un conductor parcurs de curent

electric sintra dever această forță

există ia se măsoară experimental

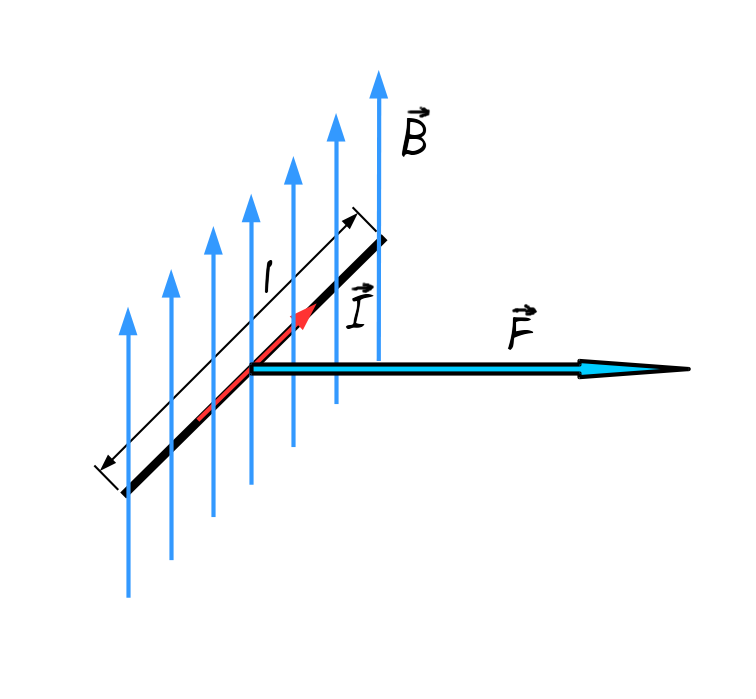
și pentru această forță electromagnetică

obținem această formulă este egal

cu lungimea activă a conductorului

parcurs de curent electric lungimea

activă înseamnă lungimea conductorului

care se află efectiv în câmpul

magnetic conductorul poate fi mai

lung dar Considerăm numai parte

din câmp este curentul electric

ce trece prin conductorul electric

și are sensul lui și b este așa

numita inducție magnetică este

un Vector ce descriem intensitatea

Câmpului magnetic despre inducția

magnetică vom discuta Mitel larg

în lecția următoare ca și comentariu

Forțele de tip electromagnetic

bineînțeles întruna sistem mai

complex dar aceste forțe electromagnetice

se folosesc în așa numitele trenuri

cu levitație magnetică aveți aici

exemplul unui tren folosită cred

că în China în Shanghai De ce este

un tren care merge pe o pernă magnetică

și are propulsie electromagnetică

datorită acestei forțe