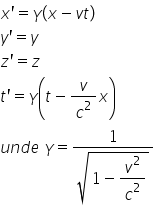Principiile Einstein. Transformările Lorentz. Relativitatea simultaneităţii.

îngeri a treia Lecție despre teoria

relativității restrânse vom discuta

despre principiile Einstein ce

stau la baza acestei teorii și

despre transformările lorentz în

lecția trecută am explicat că în

jurul anului 1900 fizica se afla

întâlnim pas pentru că se părea

că legile electromagnetismului

nu respectă principiul relativității

clasice adică ele depinde sistemul

de referință în care se face măsurătoarea

unui măsurarea unui anumit fenomen

electromagnetic precum o undă electromagnetică

de asemeni după cum am spus în

acele ție exista o serie de experimente

precum experimentul michelson care

arătau că undele electromagnetice

nu respectă transformările Galilei

acestea erau contradicții fundamentale

ce Trebuiau rezolvate și au fost

rezolvate de către Einstein în

anul 1905 prin postularea următoarelor

două principii primul principiu

al lui Einstein stipulează că legile

fizicii sunt aceleași în toate

sistemele de referință inerțială

Dacă vă duceți aminte formularea

principiul relativității clasice

Observați că aceste două principii

par să fie dentice Există o singură

diferență esențială În formularea

lor și anume În locul cuvântului

legile mecanicii mecanicii care

apărea în principiul relativității

clasice avem legile fizicii Evident

Ce înseamnă acest lucru este că

Einstein pur și simplu a postulat

că electromagnetismul este și el

invariant la alegerea sistemului

de referință inerțial după cum

experiența de zi cu zi dar nici

a înlocuit legile mecanicii cu

legile fizicii aceasta este pur

și simplu abordare curajoasă prin

care sa stabilit acest dacă vreți

echilibru relativ la experiența

noastră cotidiană în teoria fizicii

bineînțeles trebuie introdus un

anumit mecanism prin care electromagnetismul

devine și el invariant la alegerea

sistemului de referință pentru

a putea postul la faptul că toate

adică atât mecanica cât și electromagnetismul

la momentul respectiv au această

invarianți acest mecanism prin

care electromagnetismul devine

și el e varianta alegerea sistemului

de referință este conținut în cel

de al doilea postulat sau principiu

a lui Einstein care spune că viteza

luminii în vid are aceeași valoare

în toate sistemele de referință

inerțială adică nu depinde de viteza

sursei care a generat acea unde

electromagnetică luminoasă sau

Observatorului care o măsoară aceasta

este pur și simplu concluzia experimentul

lui michelson după cum vă reamintiți

experimentul michelson arătat că

în notația cele experiment si unul

este egal cu c 2 este egal cu c

3 care poate fi notat cu un c c1

c2 și C3 fiind vitae vitezele lui

Minnie în diferite dispozitive

experimentale în care viteza sistemului

de referință care era pământul

în acel caz se schimbă și Deci

Einstein pur și simplu a postulat

rezultatul experimentul lui michelson

și alt oras pe rezultate experimentale

genialitatea lui Einstein a constat

în faptul de a observa că aceste

acest Acest rezultat de Constanța

a vitezei luminii în toate sistemele

de referință inițiale schimbă legile

de transformare Galilei care vor

deveni după cum vom discuta în

curând legile de transformare Lorenz

în așa fel încât electromagnetismul

devine și el invariant în toate

sistemele de referință prima consecință

importantă la celui de al doilea

principiu este că viteza luminii

în vid devine viteza maximă de

propagare a oricărei interacțiuni

Deci un sistem fizic Real din universul

nostru nu poate depăși această

viteză pentru că pur și simplu

dacă ar depăși o atunci ar însemna

că viteza luminii ar deveni dependentă

de sistemul de referință inerțial

am avea o adunare a vitezei luminii

cu viteza sistemului de referință

în care se propagă această interacțiune

obținând astfel o anulare a principiul

al doilea Deci postul în acest

principiu al doilea obținem că

viteza maximă posibilă pentru un

sistem real fizic este acest c

Care este egal cu 3 ori 10 la 8

metri pe secundă aceste două principii

pun bazele teoriei relativității

restrânse sau speciale care devine

o generalizare a mecanicii clasice

italiene după cum vom vedea de

fiecare dată când de duce măi coaie

pentru teoria relativității restrânse

întruna numit caz particular și

anume viteze mult mai mici decât

viteza luminii obținem întotdeauna

ecuația corespondență din mecanica

newtoniana Deci mecanic a lui htonian

este valabil în continuare ia fiind

un caz particular al teoriei relativității

restrânse un alt comentariu este

că amândouă principiile și amândouă

teoriile teoria relativității și

mecanica clasică se referă doar

la sisteme de referință inerțială

în în această formulare a principiilor

de bază în particular principiul

relativității Einstein 10 ani mai

târziu adică în 1916 a oferit și

Următorul pas al teoria relativității

Numiți teoria relativității generalizate

și care face extensia legilor fizicii

la sisteme de referință neinertial

adică accelerate Deci în principiul

în teoria relativității generalizate

se face încă un pas tot de către

Einstein prin generalizarea principiului

1 în sensul că legile fizicii sunt

postulate ca fiind aceleași în

toate sistemele de referință punct

adică atât inerțial A cât și neinertial

acesta este doar un comentariu

Nu învățăm în liceu teoria relativității

generalizate faptul că viteza luminii

în vid este o constantă universală

are consecințe profunde și anume

spațiul și timpul nu mai sunt independente

așa cum erau și sunt în mecanică

sau în fizica clasică ce formează

o intrat acum una deci vorbim despre

un anumit continuu spațiu T4 dimensionali

Deci când notam x x y z și t în

mecanica clasică întotdeauna prin

x y și z înțelegeam coordonatele

ce dădeau poziția unui sistem sau

unui corp iar tei era timpul măsurat

de către un cronometru atașat sistemului

de referință inerția teoria relativității

restrânse te face parte din un

sistem de coordonate 4 dimensiunea

dimensiunea timpul de vine identificabil

spațiului ele formând o entitate

comună spații timp și aceasta deoarece

există această acest sistem preferențial

Universal lumina față de care întotdeauna

putem scrie că orice distanță sau

orice mărime sau orice lungime

orice geometrie dacă doriți este

egală cu c ori d unde c este o

constantă Universal are această

valoare Deci în raport cu acest

sistem de referință o undă electromagnetică

distanța de vine conceptuale identică

cu timp fiind legate prin o constantă

fixă universal Deci de aici rezultă

această implicație profundă dacă

vreți filozofică în abordarea al

fizicii spațiul și timpul în mecanica

clasică erau separate acum de vin

parte al al unui concept comun

transformările lorentz înlocuiesc

transformările Galilei De ce avem

aceeași situație ca și în cazul

derivării transformărilor Galilei

două sisteme de referință inertiale

s x y z și spre cu axele exprime

prin z prim în care exprimi se

mișcă cu viteza V față de sistemul

ăsta nu facem demonstrația sau

derivarea transformărilor lorentz

ia se face plecând de la cel de

al doilea principiu a lui Einstein

și dăm doar formularea lor fără

are demonstrat din nou aceasta

deoarece este o demonstrație ce

va mai complicată decât demonstrația

transformărilor Galilei Spre exemplu

plecând de la principiile despre

spațiu și timp al mecanicii clasice

și nu aduci e nici o informație

din puncte de Raul conținutului

fizic în concluzie Nu vi se cere

acestei demonstrații și nu le facem

nici noi ci pur și simplu le formulăm

transformările lorentz în care

care leagă coordonatele x si y

x prim prim D prim și timpul te

prind in sistemul spre mie cu cele

din sistemul de referință inerțial

s și anume x x y z și t din sistemul

s sunt acestea Deci te prim este

egal cu gama Care este o constantă

CEO voi introduce imediat Deci

te primeste gama înmulțit cu te

minus Van părți la ce pătrat ori

x x primeste gama x minus z y prime

este egal cu 5 de prim este egal

cu Z asta deoarece V în acest caz

particular este de a lungul axelor

comunei x și exprimă Putem generaliza

dacă vii are o direcție oarecare

înlocuind Zaku vei x și apoi apare

și în yyy8 egal înmulțit cu y minus

z y t și o parte relațiile Invers

adică prin care se leagă coordonatele

din s de cele din s prim sunt acestea

în care pur și simplu se înlocuiește

cu minus Deci transformările lorentz

între cele două sisteme de referință

inerțial se obțin prin substituția

V plus 3 minus V și invers după

cum se vede se schimbă semnul lui

z Definiția lui gama este următoarea

Deci gama el nu are nici o semnificație

fizică este pur și simplu notație

mai dacă vreți să mai degrabă decât

o definiție gama este o notație

Ea este egal acest Factor gama

cu unul împărțit la radical din

1 minus b pătrat pe c pătrat și

la am introdus pur și simplu pentru

A simplifica forma acestora formule

înseamnă concret din punct de vedere

fizic nimic această mărime eu Notați

și după cum am spus acestei ecuații

Deci transformările lorentz se

derivă se deriveaza direct din

principiile einsten particular

din cel de al doilea principiu

în care se impune ca viteza de

propagare a luminii a unei unde

electromagnetice în cele două sisteme

de referință s și s prim să fie

independentă de viteza Haideți

să vorbim acum despre consecințe

ale acestui transformărilor în

care stau la baza calculelor din

teoria relativității restrânse

prima consecință este relativitatea

simultaneității după cum am văzut

în mecanica clasică simultan simultan

itatea este absolută Adică dacă

două evenimente se întâmplă în

același moment în sistemul exprim

vor avea loc în același moment

și în sistemul Deci fie două evenimente

simultan sistemul de referință

s adică diferența temporală dintre

ele este 0 dar cu o anumită separare

în spațiu Delta x care prin definiție

este ex 2 minus x 1 este diferită

aplicăm transformările lorentz

pentru a găsi pentru a calcula

Delta D prim în sistemul de referință

spre Delta D prim prin definiție

este te prind 2 minute primul din

prima formulă a transformării Lauren

obținem că acest te prind 2 minute

primul 1 este egal cu gama de 2

minus vpc pătrați x 2 minus gama

de 1 minus b pătrat pe în minus

vpc pătrat x 1 care poate fi descrisă

în forma următoare de ăsta te plimbi

este egal cu gama de 2 minute 1

care este Delta t minus gama vpc

pătrat x 2 minus x 1 care este

Delta x dar Delta t în cazul nostru

este zero pentru că evenimentele

sunt simultan sistemul de referință

al Și de ce obține încă Delta D

prim este egal cu minus gama V

PC pătrat Delta x care este un

rezultat foarte interesant pentru

că spune că dacă două evenimente

sunt simultane în sistemul de referință

se prind nu mai sunt neapărat simultane

în sistemul de referință În ce

la sistem de referință inițial

și anumiți prin pentru că Delta

te plimb nu mai este egal cu zero

aceasta este un prim exemplu concret

pentru care această teorie se numește

teoria relativității iar relativizează

toate lucrurile care erau sau majoritatea

lucrurilor Care erau absolut în

mecanica clasică Spre exemplu simultaneitate

era absolută în mecanica clasică

devine relativă adică dependentă

de sistemul de referință în relativitatea

restrânse a lui Einstein Deci cele

două evenimente nu mai sunt simultane

în turnat sistem de referință după

cum am spus mecanica clasică este

un caz particular al teoriei relativității

restrânse aceasta înseamnă că avem

un așa numit principiul al corespondenței

care spune că mecanica clasică

sau lituaniană e un caz particular

al teoriei relativității restrânse

în limita în care viteza de propagare

a sistemului considerat este mult

mai mică decât viteza luminii Deci

în această din limită a vitezelor

foarte mici comparație cu viteza

de propagare a luminii în vid ar

trebui și trebuie să obținem rezultatele

pe ca nici clasice întradevăr simultaneitatea

Spre exemplu se obține în acest

caz si multi ani tati absolută

a mecanicii clasice pentru că pur

și simplu Dacă vei Împărțiți la

cheie este aproximativ egal cu

0 atunci gama careva readuc aminte

gama am definit ca 1 supra radical

din 1 minus b pătrat pe ce pătrat

Deci dacă vei pe ce este aproximativ

egal cu zero gama este aproximativ

egale cu De ce avem gama aproximativ

egale cu 1 dm pățit la C pătrat

este aproximativ egale cu 0 și

de și de el tot a prim devine aproximativ

egal cu 0 Deci în această limită

obține obținem simultaneitatea

și în sistemul exprima