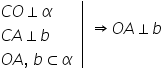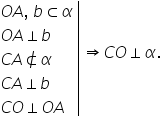Reciprocele teoremei celor trei perpendiculare
Tag-uri
Partajeaza in Google Classroom

Transcript
în continuare să discutăm despre
reciproce ale teoremei celor trei
perpendiculare Ce înțelegem prin
reciprocă a unei teoreme și am
ales acest exemplu teorema unghiului
de 30 de grade Care ce ne spune
sau enunță Fie triunghiul lemn
de numit aici b a c cu măsura unghiului
A de 90 de grade Deci dacă se dă
un triunghi dreptunghic atunci
Dacă măsura unui unghi ascuțit
de exemplu măsura unghiului c are
30 de grade atunci Ce rezultă Păi
rezultă că lungimea catetei care
se opune unghiului de 30 de grade
adică AB este egală cu jumătate
din lungimea ipotenuzei deci putem
să notăm că rezultă că a b este
egală cu bc supra 2 teorema reciprocă
Deci aceasta a fost teorema directă
teorema reciprocă ce ne spune Păi
ea ne spune că dacă ni se dă un
triunghi dreptunghic bac Deci această
parte a ipotezei rămâne o Vom copia
atunci Dacă AB este jumătate din
bc Deci dacă lungimea catetei AB
este egală cu jumătate din lungimea
catetei b c Atunci rezultă că măsura
unghiului c este de 30 de grade
plec aici măsura unghiului c egală
cu 30 de grade Ce observăm cum
am obținut teoremă reciprocă din
teoremă directă Păi am păstrat
această parte a ipotezei Iată se
vede aici Și ce am făcut am înlocuit
o parte ipotezei mă refer la această
teoremă cu concluzia Deci în loc
de măsura unghiului C egal cu 30
de grade camera în teorema directă
am scris în teorema reciprocă concluzia
iată ce era aici am trecut aici
în ipoteză și a rezultat această
parte a ipotezei că măsura unghiului
c este de 30 de grade poate cuvinte
teoremă reciprocă ne arată că lucrurile
se întâmplă și invers Deci dacă
în acest cadru ni se dă această
relație atunci rezultă această
relație prin urmare reciproca unei
teoreme se obține din teorema directă
înlocuind ipoteza sau o parte ipotezei
Cum a fost aici cu concluzia și
acum să revenim la teoremă celor
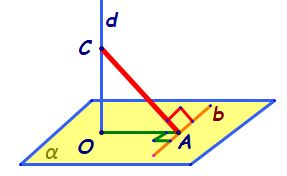
trei perpendiculare sau anunțăm
Dacă dreapta d sau să o numim c
o este perpendiculară cu Lara pe
planul alfa și dreapta a este perpendiculară
pe dreapta b o a și b sunt inclusă
în planul alfa bun atunci Ce rezultă
conform teoremei celor trei perpendiculare
rezultă că ceea e perpendiculară
pe b bun și am trasat aici și pe
desen cu roșu concluzia si a perpendiculară
pe b acum ca să obținem prima reciprocă
vom înlocui ceva anume din ipoteză
vom adăuga ipoteză faptul că ceai
perpendicular pe BD si o să știm
că dreapta c a e perpendiculară
pe dreapta b și o să ne rezulte
alt ceva concret Iată Dacă dreapta
c o e perpendiculară pe planul
alfa și ce ai perpendiculară pe
b atunci rezultă că o a perpendiculară
pe b să notăm ce o perpendiculară
pe planul alfa c a este perpendiculară
pe b dreptele o a și b unde se
află sunt incluse în planul alfa
și punctul C nu aparține planului
Alfa atunci rezultă și voi scrie
așa din reciproca teoremei celor
trei perpendiculare că o a e perpendiculară
pe b demonstrație este foarte asemănătoare
cu un demonstrația teoremei directe
Deci nu o să facem acest lucru
și aici am obținut prima reciprocă
a doua reciprocă ne spune că dacă
o a e perpendiculară pe b d oa
și b sunt inclusă în acest plan
dacă si AE perpendiculară pe b
și dacă dreapta c o a perpendiculară
pe o aia a ta de mai și 90 de grade
atunci rezultă că dreapta c o a
perpendiculară pe planul alfa să
notăm deci știm că o a e perpendiculară
pe b o perpendiculară pe dreapta
b cele două drepte o a și b sunt
inclusă în planul alfa Hai să facem
acest inclus se vadă mai bine în
planul alfa Ba nu mai știm că ceea
e perpendiculară pe b trecem și
această relație si acum este aceea
nu este inclusă în planul alfa
și mai știm că c o sau dreapta
d e perpendiculară pe atenție dreapta
o a și din reciproca teoremei celor
trei perpendiculare mă refer la
a doua reciprocă rezultă că dreapta
c o este perpendiculară pe planul
alfa nu doar pe ouă Deci rezultă
că co perpendiculară pe Alfa tot
așa demonstrația se face foarte
asemănător cu demonstrația făcută
la teoremă directă acestea au fost
cele două reciproce ale teoremei
celor trei perpendiculare