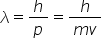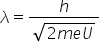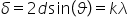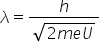Relaţia de Broglie. Difracţia electronilor. Legea Bragg.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cea de a patra lecție de fizică
cuantică vom extinde de noțiunea
de dualism unda corpuscul la cazul
particulelor elementare și anume
vom discuta de ipoteza de broșe
despre confirmarea ei experimentală
în experimente de difracție a electronilor
până acum în lecțiile precedente
de fizică cuantică am văzut cum
Plang și Einstein pe latura teoretică
și hărți contin pe latura experimentală
au demonstrat că radiația electromagnetică
are pe lângă o comportare ondulatorie
și una corpusculară comportarea
ondulatorie se vede în fenomene
de tip interferență difracție polarizare
și așa mai departe iar ceea corpusculară
în experimente de tip efect fotoelectric
extern sau imperfect contin aceasta
a fost un pas în apariția Domeniului
fizicii numit fizică cuantică totuși
leren complet pentru că fizica
în general nu se referă bineînțeles
numai la electromagnetism adică
la radiații electromagnetice 5
și la orice tip de particule precum
atomi electroni și așa mai departe
Deci trebuia pentru a avea o teoria
fizicii cuantice complete în clasă
cumva în această nouă aria fizicii
și celelalte trebuie incluse și
celelalte particule de bro am făcut
acest pas mare la sînt următoarea
ipoteză pur și simplu că și particulele
adică electroni atomi în moleculă
dar chiar și mai mult în sistemele
fizice macroscopice au pe lângă
comportarea corpusculară și una
ondulatorii bineînțeles această
ipoteză foarte îndrăzneață asta
însemna că orice corp din natura
are o undă asociată lui și că poate
fi descrisă descrisă comportarea
lui pe baza Andu la to Hide să
vedem cum se verifică practic și
cum Ce iese din această ipoteză
în primul rând trebuie făcut o
legătură între cele două laturi
ale sistemelor fizice iar ea se
face pe baza următoarelor ecuații
Deci prima ecuație care se numește
și ecuația pentru lungimea de undă
de brunet particule de impulse
pe spune că lungimea de undă a
undei asociate unei particule este
egală cu raportul dintre Constanța
plajă și impulsul particule care
poate fi scris și ca ha și împărțit
la n v această ecuație în sine
nu era nouă pentru că pentru fotoni
Einstein a demonstrat că energia
e Care este egal cu 1 conform ipotezei
planck este de asemenea egală cu
produsul dintre impulsul fotonului
și viteza luminii în vid de aici
îmi scrii imediat că c împărțit
la nu este egal cu h împărțit la
pe de unde rezultă că pentru orice
foto nu avem Lambda egal cu h împărțit
la b Deci în sine această ecuație
nu era nouă la fel și cea de 2
ecuație de legătură dintre o unde
și o particulă și anume că frecvența
unde asociate unei particule de
energie este egală cu raportul
dintre Constanța Plec și energia
particule la fel această ecuație
este ecuația Frank ecuația de la
baza ipotezei Prank și anume că
cuanta de energie are energia hazliu
de acestei ecuații nu sunt noi
ce este nou Este domeniul de aplicabilitate
pe care de Brăila definit și anume
că intră o dată începând cu de
voi numai aplicăm Ce este 2 cracii
doar pentru fotolii și radiații
electromagnetice Deci ci și pentru
orice sistem fizic atât microscopic
cât și macroscopic adică electronii
atomului cule dar în principiu
și mașina dumneavoastră are unde
asociată a care va avea lungimea
de undă și frecvența legată de
impulsul și energie cinetică a
mașinii prin aceste ecuații Deci
întradevăr ipoteze o ipoteză foarte
îndrăzneață Haideți întâi să vedem
de ce dacă orice corp are o undă
noi nu vedem o comportare ondulatorie
a corpurilor din jurul nostru Deci
Să considerăm următoarele 2 exemple
particulare în primul rând Să considerăm
un corp microscopic Adică o particulă
elementară în cazul acesta Deci
un electroni este accelerați pentru
a fi puse în mișcare de o diferență
de potențial relativ mic 100 de
volți și atunci să calculăm lungimea
de undă asociat acestui sistem
fizic microscopic în mișcare electron
accelerat Deci plecăm de la următoarea
ecuație variației energiei cinetice
este egală cu lucrul mecanic pentru
diferență de potențial mică precum
aceasta energia cinetică a electronului
este ne relativista va poate fi
scrisă cu formula clasică mv pătrat
împărțit la 2 minus 0 deltaice
și minus energia cinetică inițială
dar presupunem că electronul este
accelerat din poziția inițială
în repaus Deci energia cinetică
inițial este 0 ce obținem mv pătrat
pe 2 este egală cu lucrul mecanic
efectuat de către sistemul electric
care aplica această diferență de
potențial Deci sarcină electrică
Makita cu diferența de potențial
Deci bineînțeles extrage viteza
fi Deci Viteza va fi 2 e împărțită
la masa electronului de Unde putem
calcula mw decembrie adică impulsul
electronului va fi egal cu radical
din 2 m u și apoi Aplicând ecuația
plang pe care o are amintesc îl
am Da este egal cu h împărțit la
mw obținem că lungimea de undă
electronului în acest caz va fi
Hash împărțit la radical din 2
mulți tool cu masa electronului
sarcina electronului și diferența
de potențial de 100 de volți înlocuind
valori acestor parametri o ține
încă lungimea de undă a electronului
în acest caz după un calcul va
fi egală cu 0 nanometri vă reamintesc
na nu e definiția sau notația pentru
10 la minus 9 Deci 0 ori 10 la minus
9 metri aceasta este lungimea de
undă a electronului accelerat în
această diferență de potențial
este între adevărul lungime de
undă foarte mică totuși dobroi
a sesizat că în principiu ar putea
avea consecințe măsurabile deși
foarte mici aceste lungimi de undă
pot produce efecte măsurabile precum
distracție electronilor în rețeaua
atomică a unui cristal aceasta
deoarece într un cristal distanța
dintre atomii e de ordine 10 la
minus 10 m adică 0 nanometri Care
este comparabil cu lungimea de
undă ipotetică a electronului din
acest calcul simplu în concluzie
dacă trimitem un fascicul de electroni
cu această lungime de unda sau
lungime de undă în jur de această
valoare pe o rețea cristalină atomică
ar trebui să observăm fenomene
de difracție adică franci după
cum vă amintiți maxim și Minnie
lăsând deocamdată acest punct de
o parte asupra căreia Vom reveni
și anume faptul că rezultă că lungimea
de undă asociată electronului este
mică dar în principiu măsurabilă
și producând efecte măsurabile
să ne întoarcem la sisteme și mai
mari Deci al doilea caz să consideri
în al doilea ca Să considerăm un
sistem fizic macroscopic Spre exemplu
o minge de tenis care are masă
standardizată de aproximativ 60
de g Care este elvita de un jucător
cu o viteză relativ mare pentru
un corp microscop de 100 de m pe
secundă Haideți să calculăm lungimea
de undă ipotetică asociată unui
astfel de sistem adică această
minge de tenis în mișcare aplicăm
din nou ecuația de bro pentru lungimea
de undă a unui corp Land egal cu
h împărțit la n v și locuim valoarea
constantei planck valoarea masini
mingii și anume 0 kg înmulțită cu
viteză ai 100 de metri pe secundă
și Deci obținem că lungimea de
undă asociată aceste mingi de tenis
va fi de aproximativ 10 la minus
34 m Aceasta este o lungime de
undă extraordinar de mic wasel
de lungime de undă a imposibil
de detectat chiar și cu cele mai
moderne aparate din Laboratoarele
noastre curent pentru a exemplifica
la ora actuală vitezele cele mai
mari ale particulelor se obțin
în acceleratorul large hadron collider
în care protonii sunt accelerați
la energii de energii cinetice
de 14 Terra electronul volți Adică
dacă calculam Terra înseamnă 10
la a 12 Deci 14 ori 10 la doi electroni
volți pentru a trece în sistemul
internațional de unități de măsură
trebuie să trecem de la ASUS uitate
electron volt la jul asta se face
prin relația un Joule este egal
cu un sarcină electrică elementară
1 ori 10 la minus 19 coulomb înmulțit
cu un volt De ce un John John este
energia acumulată de un electron
accelerat într o diferență de potențial
de un volt și de ce obținem că
în această super accelerator despre
care am mai vorbit în lecțiile
de teoriei relativității Deci în
acest super ale accelerator protonii
au această energie cinetică de
2 Micro Juli Care este energia
imensă pentru particular cât de
mică pe cu un Proton totuși dacă
calculăm lungimea de undă pentru
această energie cinetică obținem
o valoare a lungimii de undă a
protonului de un milion de ori
mai mare decât o astfel de lungime
de undă în concluzie motivul pentru
care un mașina dumneavoastră poate
avea o lungim de sotia ta Și totuși
noi să nu observăm efecte ondulatorii
ale acestei mașini este pentru
că ele au loc la o scară la care
capacitatea noastră de observare
chiar și cu cele mai bune instrumente
moderne este depășită de ce aceste
efecte sunt complet invizibile
și ne observabile pentru noi acum
să revenim la particulele microscopice
precum acest electroni în care
în principiu efectele de tip de
bro efectele ondulatorii ale particulelor
pot fi observate adică se poate
încerca observarea unei unui fenomen
ondulator iu precum difracția pentru
o particulă precum electron acesta
experiment a fost făcut de către
de avion și chiar măr deci difracția
electronul a fost măsurată experimental
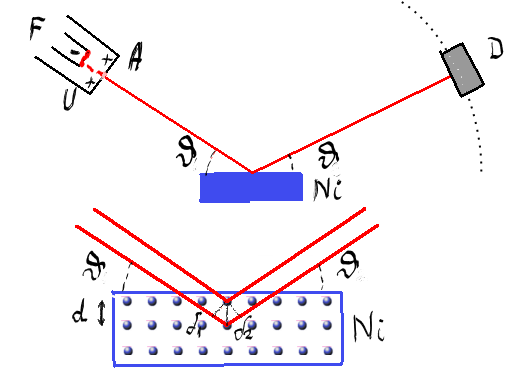
în experimentul de avion Gherman
a cărui schema simplificată o vedeți
în acest desen și o să le explic
pe scurt Deci ce avem notat cu
F este un filament Care este conectat
la o sursă și de se încălzește
Când devin incandescente el începe
să imităm prin ca altele și electroni
iar acești electroni sunt accelerați
apoi în diferența de potențial
pe care filamentul îl are relativ
la anodul A deci anodul a este
încărcat pozitiv De ce electronii
vor fi accelerații în acest spațiu
datorită diferenței de potențial
dintre filament și anulat iar apoi
ei se îndreaptă către un cristal
de nichel Deci ce vedeți aici cu
acest pătrat albastru hașurat este
un cristal de Nicol care ne experimentare
posibilitatea de a se roti in jurul
axului propriu mai exact acestui
unghi de incidență și apoi de împrăștiere
poate fi variat și în final bineînțeles
avem și un detector de electroni
notat cu d care în experimentul
dar sunt Gherman se poate mișca
pe o șină circulară Pentru a măsura
electronii împrăștiați elevul avarii
unghiuri tata prima măsurătoare
făcută de către m a a fost aceea
că pentru veri unghiuri de incidență
tetra se obțin maxime și minime
ale curentului direct roni împrăștiați
deci pe scurt dacă se reprezintă
se măsoară și apoi se reprezintă
grafic intensitatea curentului
de electroni în detectorul de la
verii unghiuri teta de împrăștiere
se obține o figură tipică de difracție
adică obține maxime și minime Deci
Fran și apoi în a în a doua etapă
a experimentului se menține unghiul
te taie fix și se variază tensiunea
de accelerare Deci la fix dar la
o tensiune de accelerare o variabilă
se obține iarăși o figură de difracție
o comportare distractivă a electronilor
Măsurați în de mai exact dacă se
face graficul intensității electronilor
Măsurați în detectorul de ca funcție
de unde să scriu haideți aici radical
din u unde au este tensiunea de
accelerare se obține iarăși fracții
iarăși franje adică maxime și minime
ale acestor electronice o comportare
de tip de fracție a electronilor
în mai multe variabile Haideți
să vedem cum se poate descrie această
comportare mărind cristalul de
Nicol putem să ne imaginăm următoarea
situație în Crystal avem rețeaua
cristalină Adică atomii sunt dispuși
în această structură cristalină
pe care cade această radiație această
acest fascicul de electroni care
e făcut din electronică zând toți
la un unghi data de ce un ghiul
stătea este unghiul de incidență
al electronilor pe cristal dacă
notăm cu d distanța dintre straturile
de atomi din distanța Inter atomică
atunci putem observa că diferența
de drum în unele tronc se împrăștie
pe primul strat de atomi și electroni
și se împrăștie pe al doilea strat
de atomi va fi egală cu suma dintre
aceste două segmente Deci Delta
1 notăm cu Delta unul și Delta
2 aceste două segmente și atunci
Delta diferența de drumul Optic
va fi egal cu Delta 1 plus Delta
2 dar ele sunt egale b c este egală
cu 2 Delta 1 iar apoi putem observa
că dacă acesta este unghiul teta
de incidență atunci aceste două
unghiuri sunt și ele tata Da Și
atunci de Delta 1 va va sinus de
teta va fi egal cu Delta unul împărțit
la D Deci avem că diferența de
drum Optic între acest acești doi
electroni va fi egal sau diferența
de drum între acești doi electroni
va fi egală cu doi de sinus de
teta pentru a maxim după cum știm
din lecțiile de difracție trebuie
să avem condiția ca diferența de
drum să fie ca portland deci aceasta
este așa numita ecuație prag pentru
obținerea maximelor de difracție
a electronilor un dispozitiv de
tip de avion Gherman iarăși important
De notat este că acest loc dacă
are lungimea de undă a electronilor
după cum am demonstrat este egal
cu h împărțit la radical din 2
m e u Deci Lambda este direct legat
de tensiunea de accelerare cu celelalte
fiind constant în concluzie poziția
acestor maxim unghiurilor ta este
dat de lungimea de undă adică de
tensiunea de accelerare și de distanța
dintre nivelele între straturile
de distanța interatomice în particular
dacă folosim după cum am calculat
precedent în minutele precedente
o tensiune de accelerare de 100
de v după cum am văzut Aplicând
această ecuație obținem valoarea
lungimii de undă electronilor de
0 nanometri Deci cunoaștem da Apoi
măsurăm Constanta scuzați că măsurăm
poziția ta a primului maxim Deci
pentru ca egal cu unu primul maxim
experimental poziția unghiului
tata este 65 de grade în cazul
Chris a lui Daniel și atunci putem
extrage direct distanța Inter atomică
pentru cristalul de nichel de 9
nanometri în concluzie experimentul
davisson germer a demonstrat Că
întradevăr electronii se comportă
ondulatoriu avem fenomene de difracție
clare în mai mulți parametri ce
depind mai mult de mai mulți parametri
ai electronilor pe cristale de
nichel și mai mult ca și aplicație
practică această proprietate electronilor
poate fi folosită pentru măsurarea
caracteristicilor rețelei cristaline
în cazul acesta distanța interatomice
a cristalului de nichel