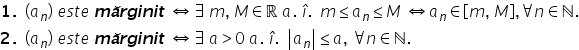Șiruri mărginite
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție discutăm despre
șiruri mărginite și începem cu
o definiție un șir a n se numește
mărginit superior dacă există un
număr real m astfel încât a n să
fie mai mic sau egal cu m oricare
ar fi numărul natural n cu alte
cuvinte un șir este mărginit superior
dacă toți termenii șirului sunt
mai mici sau egali cu un număr
real m acest număr m se numește
majorant al șirului un șir a n
se va numi mărginit inferior dacă
există un număr real a mic astfel
încât m să fie mai mic sau egal
cu a n oricare ar fi numărul natural
n altfel spus un șir este mărginit
inferior dacă toți termenii șirului
sunt mai mari sau egal cu o anumită
valoare m acest număr n mic se
numește Minora and al șirului mama
spune că un șir a n este mărginit
dacă a n este mărginit superior
și inferior prin urmare a n este
mărginit dacă există două numere
reale M mic M mare astfel încât
m mic e mai mic sau egal decât
a n mai mic sau egal cu M mare
oricare ar fi numărul natural n
dar această condiție se mai poate
Transcrie și astfel există două
numere reale M mic M mare astfel
încât a n să aparțină intervalului
a mic M mare oricare ar fi n număr
natural Așadar dacă Reprezentăm
pe o axă un șir mărginit toți termenii
acestuia trebuie să aparțină unui
interval de forma M mic M mare
Iată aici avem termenii șirului
a n în cazul în care a n este mărginit
toți termenii trebuie să aparțină
unui interval acum orice interval
poate fi inclus întru un interval
mai mare centrat în 0 Iată putem
să includem acest interval între
un interval de formă a minus a
A deci avem un interval Simetric
centrat în 0 Haideți să scriem
intervalul M mic M mare este inclus
în intervalul minus a a unde a
este un număr pozitiv dacă termenii
șirului a n aparțin acestui interval
M mic M mare atunci a n aparține
și intervalului minus a a dar această
condiție este echivalentă cu următoarea
minus a mai mic sau egal decât
n mai mic sau egal decât a iar
această relație se mai poate Transcrie
și astfel modul de a n este mai
mic sau egal decât a Așadar această
condiție pe care am scris o Aici
se mai poate scrie și astfel există
a un număr pozitiv de data aceasta
astfel încât modul de a n să fie
mai mic sau egal cu a oricare ar
fi n număr natural Așadar pentru
a studia mărginirea unui șir arătăm
că este îndeplinită una din aceste
trei condiții un șir care nu este
mărginit se numește nemărginit
să vedem în continuare câteva exemple
să vedem dacă este mărginit următorul
șir a n unde a n este egal cu 5
n număr natural nenul Acesta este
un șir constant prin urmare toți
termenii șirului valoarea 5 Așadar
acest șir este mărginit pentru
că modul de a n este mai mic sau
egal cu 5 oricare ar fi n număr
natural nenul Așadar rezultă că
șirul a n este mărginit un alt
exemplu avem șirul b n unde b n
este egal cu minus 3 Dacă n este
par 3 Dacă n este impar Așadar
termenii șirului pot avea valoarea
3 sau minus 3 prin urmare Acesta
este un șir mărginit pentru că
b n aparține intervalului minus
3 3 oricare ar fi n număr natural
nenul sau ar fi putut să scriem
ca și mai sus modul de b n mai
mic sau egal cu 3 Așadar șirul
b n este mărginit să vedem următorul
șir xn unde x n este egal cu n
n număr natural nenul observăm
Așadar că șirul acesta este de
fapt șirul numerelor naturale 1
2 3 4 5 și așa mai departe să vedem
dacă acesta este un șir mărginit
putem să intuim faptul că acest
șir va fi nemărginit pentru că
el nu are o margine superioară
cu cât crește rangul termenilor
cu atât va crește și valoarea acestora
Deci cu cât merge mai departe în
șir termenii acestuia tot cresc
prin urmare șirul nu va fi mărginit
superior dar Haideți să demonstrăm
acest lucru 100 demonstrăm prin
reducere la absurd presupunem că
Accent este mărginit dacă este
mărginit înseamnă că există un
număr pozitiv a astfel încât modul
de x n să fie mai mic sau egal
cu a oricare ar fi n număr natural
nenul adică există un apozitiv
a astfel încât În cazul nostru
x n este egal cu n iar modul de
n este pentru că na pozitiv n mai
mic sau egal decât a oricare ar
fi n număr natural nenul să vedem
dacă este adevărată această afirmație
în cazul în care aș alege a n ca
fiind partea întreagă din a plus
1 alegem partea întreagă pentru
că an trebuie să fie număr natural
partea întreagă a numărului a la
care se adaugă 1 este mai mare
decât a prin urmare nu pentru orice
număr natural n are loc această
inegalitate n mai mic sau egal
cu a iar în cazul în care n este
partea întreagă din a plus 1 atunci
el va fi mai mare decât ei așa
dar această condiție nu este îndeplinită
pentru orice număr natural n înseamnă
că presupunerea noastră este falsă
prin urmare rezultă că șirul x
n este nemărginit să facem în continuare
niște exerciții Studiați mărginirea
șirurilor avem aceste patru șiruri
în fiecare caz n este număr natural
diferit de 0 și începem cu punctul
a avem șirul x n egal cu 3 n minus
2 supra n Haide să calculăm câțiva
termeni ai acestui șir primul termen
este X1 egal cu 3 ori 1 minus 2
1 supra 1 adică 1 x 2 este 3 ori
2 6 minus 2 4 supra 2 egal cu 2
x 3 este 3 ori 3 9 minus 2 7 supra
3 și mai calculăm un termen x 4
este 3 ori 4 12 minus doi zece
supra 4 se mai simplifică și ne
dă cinci pe doi observăm Așadar
că toți termenii acestuia sunt
pozitivi prin urmare Putem să scriem
că zero este mai mic sau egal decât
x n observăm Așadar că șirul este
mărginit inferior Haide să vedem
dacă reușim să arătăm că șirul
este mărginit superior pentru aceasta
mai scrie încă o dată formula termenului
general x n egal cu 3 n minus 2
supra n o să scriem această fracție
ca o diferență de două fracții
și Avem 3 n pe n minus 2 pe n egal
cu 3 minus 2 supra n n este număr
natural prin urmare 2 supra n este
un număr pozitiv dacă din 3 scădem
o valoare pozitivă obținem un număr
mai mic decât 3 prin urmare șirul
nostru x n este mărginit superior
de trei așa dar putem să scriem
x n mai mic decât 3 rezulta ca
șirul x n este mărginit trecem
la punctul b avem șirul x n egal
cu 4n plus 9 supra n plus 2 se
poate observa imediat că toți termenii
acestui șir sunt pozitivi prin
urmare Putem să scriem direct că
zero este mai mic sau egal decât
x n prin urmare șirul este mărginit
inferior să vedem dacă reușim să
demonstrăm că șirul este mărginit
superior pentru aceasta o să mai
scriu încă o dată x n egal cu 4
n plus 9 supra n plus 2 egal acum
în loc de 9 o să scriem 8 plus
1 supra n plus doi din primii doi
termeni dăm factor comun pe patru
și avem patru pe lângă n plus 2
plus 1 supra n plus 2 egal 4 pe
lângă n plus 2 supra n plus 2 plus
1 supra n plus 2 se simplifică
n plus 2 și obținem patru plus
unu supra n plus doi acum această
fracție 1 supra n plus 2 este o
fracție subunitară întrucât en
ia valori mai mari sau egale cu
1 și atunci tot acest număr va
fi mai mic decât 4 plus 1 care
este egal cu 5 Așadar șirul x n
este mai mic decât 5 Putem să scriem
aici prin urmare șirul este mărginit
atât inferior cât și superior Așadar
x n este mărginit continuăm cu
punctul c avem x n egal cu minus
1 la n supra n pătrat plus 2 de
data aceasta Haideți să calculăm
modul de x n și avem modul din
minus 1 la n supra n pătrat plus
2 egal cu 1 supra n pătrat plus
2 și această fracție este subunitară
prin urmare șirul nostru este mărginit
rezultă xn mărginit și continuăm
cu punctul A de avem x n egal cu
radical din n plus 2 minus radical
din n plus 1 știind că n plus 2
este mai mare decât n plus 1 din
moment ce an este număr natural
prin urmare radical din n plus
2 va fi mai mare decât radical
din n plus unu înseamnă că această
diferență radical din n plus 2
minus radical din n plus 1 este
pozitivă prin urmare x n este mai
mare decât 0 sau Putem să scriem
0 mai mic ca x n Așadar șirul este
mărginit inferior de 0 și acum
o Să arătăm că șirul este mărginit
superior continuăm alăturat o să
mai scriu încă o dată x n egal
cu radical din n plus 2 minus radical
din n plus 1 de data aceasta o
să amplificăm această expresie
cu expresia conjugată adică amplificăm
cu radical din n plus 2 plus radical
din n plus 1 și o să obținem radical
din n plus 2 plus radical din n
plus 1 pe lângă radical din n plus
2 minus radical din n plus 1 supra
radical din n plus 2 plus radical
din n plus 1 egal la numărător
avem n plus 2 minus n minus unu
Atenție la semne supra radical
din n plus 2 plus radical din n
plus 1 egal 1 supra radical din
n plus 2 plus radical din n plus
1 Acum putem să mă ajută această
fracție cum 1 supra radical din
n plus 1 plus radical din n plus
1 Iată radical din n plus 2 este
mai mare decât radical din n plus
1 prin urmare numitorul primei
fracții este mai mare decât numitorul
aceste fracții dar cele două fracții
au același numărător Așadar fracția
cu numitorul mai mare este mai
mică decât fracția cu numitorul
mai mic așa dar putem să facem
această majorare și obținem în
continuare egal cu 1 supra 2 radical
din n plus unu care se mai poate
scrie 1 supra 2 ori 1 supra radical
din n plus 1 această fracție este
subunitară Deci tot Acest număr
este mai mic decât 1 supra 2 am
arătat Așadar că șirul x n este
mai mic decât 1 pe 2 putem să completăm
aici în urmare șirul x n este mărginit
atât inferior cât și superior Deci
x n este mărginit