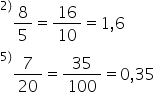Transformarea fracțiilor ordinare cu numitorul putere a lui 10 în fracții zecimale. Aplicație

să facem acum un exercițiu în care

vom transforma fracții ordinare

în fracții zecimale Scrieți următoarele

fracții ordinare ca fractii zecimale

și mi se dă această fracție 7 supra

2 și vrem să o scriem ca număr

zecimal bun însă Noi am învățat

să scriem o fracție ordinară ca

fracție zecimală dacă numitorul

este putere a lui 10 adică 10 100

1000 și așa mai departe însă aici

numitorul este 2 Păi cum putem

să ajungem de la doi la zece putem

să amplificăm aici cu cât cu cinci

și ce vom obține avem cinci ori

doi ne dă 10 Degeaba am obținut

numitorul 10 7 ori 5 ne dă 35 35

supra 10 se scrie 3 de ce atacă

prin amplificare putem ca dintr

o fracție ordinară care nu a numitorul

putere a lui 10 să obținem o fracție

ordinară cu numitorul putere a

lui 10 alt exemplu 8 supra 5 Păi

cu cât să amplificăm acum Ce număr

înmulțit cu 5 ne dă 10 foarte simplu

vorbim de numărul doi Deci vom

avea numitorul 10 8 ore 216 Deci

obținem 16 pe 10 adică 1 sau 3 supra

4 Păi unde sa vedem acum Ce număr

înmulțit cu 4 de să notăm Ce număr

înmulțit cu 4 ne dă 10 aici vorbim

de un număr natural există un asemenea

număr natural care înmulțit cu

4 să ne dea 10 RON există însă

putem să obținem atunci 100 sigur

25 ori 4 ne dă o deci putem aici

să ștergem semnul întrebării și

să scriem numărul 25 și vom obține

25 ori 4 avem 125 ori 3 ne dă 7575

supra 100 înseamnă 0 un alt exemplu

să calculăm să scriem acum ca fracție

zecimală 31 supra 25 Păi cu Cât

stă amplificăm această fracție

pentru servo m de simplificat nu

o putem simplifica toate un acum

au fost Fracții reductibile pentru

că și prin simplificare în anumite

situații putem să ajungem la un

numitor putere a lui 10 Deci tot

așa trebuie să amplificăm Păi ce

număr înmulțit cu 25 ne dă o putere

a lui 10 Păi am văzut mai sus că

pa 25 ne dă 100 deci putem ai să

ștergem și să scriem direct cum

precum cu 4 și vom avea numitorul

tot 104 ori 31 ne dă 124 124 pe

100 înseamnă 1 sau dacă avem de

exemplu un 7 supra 20 Cu cât se

amplifică tot așa avem o fracție

ireductibilă Păi ce număr înmulțit

cu 20 ne dă de exemplu 105 5 ori

20 ne da 100 Deci vom avea aici

105 ori 7 35 35 supra 100 ne de

0 încă un exemplu cu 1 supra 50

aici e ușor să ne dăm kaboom amplifica

cu doi și vom avea doi supra 100

carene de 0 dacă avem în 5 supra

50 Păi și această fracție poate

fi amplificată cu doi și vom obține

10 supra 100 sau putem să o simplificăm

prin cinci și vom obține 1 supra

10 care de de 0 iar dacă am fi amplificat

cu doi de nota mai și doi am fi

obținut 10 supra 100 simplifica

prin 10 Deci tot fracția 1 pe 10

ca aici adică 0 ce credeți toate

fracțiile pot fi amplificate sau

simplificate astfel încât să obținem

o fracție ordinară cu numitorul

putere a lui 10 pe Haide să luăm

acest exemplu 1 sub trei cu cât

să amplificăm această fracție pentru

copt servi 1.008 fracție ireductibilă

nu o putem simplifica Deci cu cât

sau amplificăm astfel încât acest

număr înmulțit cu trei să ne dea

10 Păi nu există niciun număr natural

care înmulțit cu 3 să ne dea 10

dar 100 tot așa nu există un asemenea

număr necta nici pentru 1000 de

fapt oricât de multe zerouri am

adăuga aici numărul format nu se

va împărți niciodată exact la 3

asta înseamnă că nu există nici

un număr natural care înmulțit

cu 3 să ne dea putere o să ne dea

o putere a lui 10 cu alte cuvinte

nu toate fracțiile pot fi amplificate

sau simplificate în așa fel încât

să obținem numitorul putere a lui

10 însă și această fracție ordinară

poate fi scrisă ca fracție zecimală

numărul care se obține este diferit

față de acest de aceste numere

zecimale el intră întru altă categorie

acum Dacă tot am pomenit putem

să notăm de curiozitate este este

egal cu 0 și despre aceste numere

zecimale periodice vom învăța ceva

mai târziu ca să concluzionăm Fiind

dată o fracție ordinară putem ajunge

la o fracție ordinară cu numitorul

putere a lui 10 doar dacă numitorul

fracției respective are doar puteri

ale lui 2 sau 5 cum am avut aici

am avut doi aici Am avut cinci

patru este 2 la a doua 25 este

5 la a doua 20 este 5 ori 4 adică

5 ori 2 la a doua observăm peste

tot în numitorii au fost Formați

doar din puteri ale lui 5 cum e

aici și puteri ale lui doi doar

în asemenea situații putem să ajungem

de la o fracție dată la o fracție

ordinară care să aibă numitorul

putere a lui 10