Apotema piramidei
Tag-uri
Partajeaza in Google Classroom
Teorie: Apotema piramidei Descarcă PDF
Apotema piramidei
Poligon regulat = poligon cu toate laturile și toate unghiurile congruente.
Piramidă regulată = piramidă cu baza poligon regulat și muchiile laterale congruente.
Piramidă patrulateră regulată= piramida cu baza pătrat și muchiile laterale congruente.
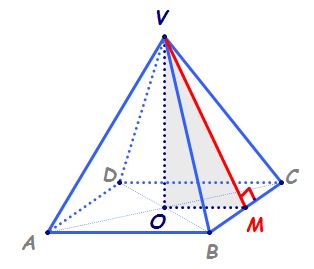
VABCD- piramidă patrulateră regulată;
- Muchiile bazei: AB=BC=CD=DA
- Muchiile laterale:VA=VB=VC=VD
- Baza piramidei este pătratul ABCD.
- Fețele laterale sunt triunghiuri isoscele.
- Punctul O este centrul cercului circumscris bazei.
Înălțimea unei piramide regulate este distanța de la vârful piramidei la centrul cercului circumscris bazei (în figura de mai sus, înălțimea piramidei este VO).
Apotema piramidei este înălțimea unei fețe laterale (distanța de la vârful piramidei la o muchie a bazei); în figura de mai sus, apotema este VM (VM este perpendiculară pe BC).
- Important: triunghiul VBC este isoscel, prin urmare înălțimea VM este și mediană, deci punctul M este mijlocul segmentului [BC].
Apotema bazei este distanța de la centrul cercului circumscris bazei la o muchie a bazei; în figura de mai sus, OM este mediană în triunghiul isoscel BOC, deci OM este și înălțime; prin urmare, apotema bazei este OM.
Concluzii:
Piramidă triunghiulară regulată= piramida cu baza triunghi echilateral și muchiile laterale congruente.
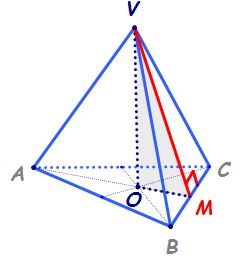
VABC- piramidă triunghiulară regulată;
- Muchiile bazei: AB=AC=BC
- Muchiile laterale:VA=VB=VC
- Baza piramidei este triunghiul echilateral ABC.
- Fețele laterale sunt triunghiuri isoscele.
- Punctul O este centrul cercului circumscris bazei.
Înălțimea unei piramide regulate este distanța de la vârful piramidei la centrul cercului circumscris bazei (în figura de mai sus, înălțimea piramidei este VO).
Apotema piramidei este înălțimea unei fețe laterale (distanța de la vârful piramidei la o muchie a bazei); în figura de mai sus, apotema este VM (VM este perpendiculară pe BC).
- Important: triunghiul VBC este isoscel, prin urmare înălțimea VM este și mediană, deci punctul M este mijlocul segmentului [BC].
Apotema bazei este distanța de la centrul cercului circumscris bazei la o muchie a bazei; în figura de mai sus, AM este mediană în triunghiul echilateral ABC, deci AM este și înălțime; prin urmare, apotema bazei este OM.
Concluzii: