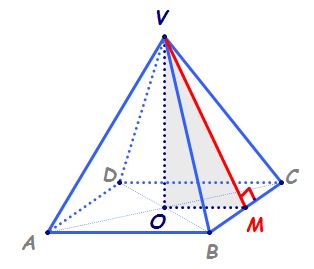
Piramida patrulateră regulată (descriere și desfășurare)

să discutăm acum despre piramida

patrulateră regulată Ce înțelegem

prin o piramidă patrulateră regulată

Dacă ea se numește patrulateră

înseamnă că baza este un patrulater

și dacă ea se numește regulată

înseamnă că avem îndeplinite două

lucruri primul lucru bază este

un patrulater regulat adică un

pătrat și al doilea lucru muchiile

laterale sunt congruente să vedem

cum arată o asemenea piramidă bază

este cum am spus pătrat muchiile

bazei sunt ab bc cd și AD iar muchiile

laterale sunt va vb vc și vd bun

Cum sunt fețele laterale Păi am

spus că bază este pătrat cu alte

cuvinte muchiile bazei sunt congruente

iar fețele laterale sunt triunghiuri

isoscele înseamnă de fapt că muchiile

laterale sunt congruente adică

V a este congruent cu a b congruent

cu BC congruent cu vd de reținem

că bază este pătrat și fețele laterale

sunt triunghiuri isoscel în continuare

vom face câteva construcții între

o piramidă patrulateră regulată

cine se dă piramida V a b c d mai

întâi să determinăm centrul cercului

circumscris bazei având în vedere

că bază este pătrat Unde se află

Centrul cercului circumscris bazei

se află la intersecția diagonalelor

Deci trebuie să construim diagonalele

acestui pătrat Iată putem să numim

punctul de intersecție cu o și

o este centrul cercului circumscris

bazei acum Dacă vom Uni vârful

piramidei cu punctul O ce vom obține

este înălțimea în piramidă Deci

v o este înălțimea în această piramidă

și anume înălțimea unei piramide

regulate este distanța de la Vârful

piramidei la centrul cercului circumscris

bazei absolut aceeași definiție

ca și la piramida triunghiulară

regulată să construim Acum deci

mai întâi să scriem aici Că v o

înălțimea piramidei să construim

acum apotema piramidei apotema

piramidei este distanța de la Vârful

piramidei la o muchie a bazei Deci

trebuie să ducem o perpendiculară

din vârful piramidei pe un muchia

bazei și să ducem perpendiculara

din b pe BC Cum facem acest lucru

pe foarte simplu putem să alegem

m mijlocul segmentului BC Deci

BM este congruent cu MC si Ce reprezintă

vm dacă unim pe V cu m ce vom obține

Păi avem de fapt mediană în triunghiul

a b c cu triunghiul este isoscel

cu vârful în v înseamnă că mediană

avem este și înălțime de ce avem

aici 90 de grade asta înseamnă

că bem e distanța de la V la latura

la muchia bazei BC trecem aici

că vm este apotema în această piramidă

să construim acum și apotema bazei

Iată apotema bazei este distanța

de la centrul cercului circumscris

bazei la o muchia bazei să construim

distanța d se duce o perpendiculară

din o pe latura bc Dacă unim însă

pe o cu m și chiar o să îl unesc

ce vom obține este cumva o m perpendiculară

pe BC pe ce reprezintă om în triunghiul

a c b Iată o este mijlocul segmentului

ac M este mijlocul segmentului

BC înseamnă că om Ce este linie

mijlocie în triunghiul a c b e

dacă e linie mijlocie înseamnă

că om este paralelă cu AB Cum sunt

dreptele AB și BC sunt perpendiculare

avem aici 90 de grade cam 1000

este paralelă cu AB înseamnă că

și om este perpendiculară pe BC

deci putem să trecem ca avem aici

Unul drept bun asta înseamnă că

om să notăm este apotema bazei

acestea au fost cele trei construcții

pe care am vrut să le facem în

piramida patrulateră regulată iar

putem să facem să dispară diagonalele

bazei ele trebuiau urcăm să fie

trecute punct tot acum piramida

știm deja Cum să o notăm începem

cu vârful avem V a b c d și să

vedem în continuare desfășurarea

unei asemenea piramide ca să vedem

desfășurarea apăsând pe butonul

de deschidere Iată aceasta este

desfășurarea unei piramide patrulatere

regulate fețele laterale cele patru

triunghiuri sunt triunghiuri isoscele

iar bază este pătrat