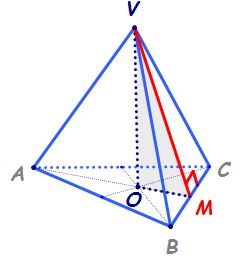
Piramida triunghiulară regulată (descriere și desfășurare)
Tag-uri
Partajeaza in Google Classroom

Transcript
în continuare vom discuta despre
piramida triunghiulară regulată
însă mai înainte să vedem ce înseamnă
piramidă regulată fie că este triunghiulară
patrulateră hexagonală o piramidă
regulată este o piramidă cu baza
poligon regulat și muchiile laterale
sunt congruente atunci ce înseamnă
piramidă triunghiulară regulată
e bine este o piramidă cu baza
triunghi pentru că se numește triunghiulară
iar triunghiul trebuie să fie un
poligon regulat asta înseamnă că
avem baza triunghi echilateral
și muchiile laterale sunt congruente
iar piramida triunghiulară regulată
este o piramidă cu baza triunghi
echilateral și cu muchiile laterale
congruente astfel triunghiul m
n p este triunghi echilateral Reprezentăm
acest lucru pe figură iar fețele
laterale sunt triunghiuri isoscele
Deci q m este congruent cu qn iar
q p este și el congruent cu qn
cu alte cuvinte muchiile laterale
sunt congruente Haide să vedem
muchiile laterale sunt q m q n
și q p și muchiile bazei sunt și
ele congruente muchiile bazei sunt
i m n p e n și m p acum fețele
laterale sunt triunghiurile q m
n q n p și q p m iar bază este
dată de triunghiul MNP în continuare
o să facem trei construcții foarte
importante pentru o piramidă triunghiulară
regulată și de aceea cel mai bine
este să începem cu construcția
piramidei mai întâi construim baza
piramidei triunghiulare triunghiul
a b c d și nu pare că este un triunghi
echilateral noi Considerăm că avem
aici un triunghi echilateral știind
că atunci când desenăm în plan
corpuri geometrice distanțele nu
se păstrează după ce am trasat
triunghiul de la bază urmează să
construim centrul cercului circumscris
bazei însă Cum Noi avem un triunghi
echilateral nu știm că pentru a
construi centrul cercului circumscris
bazei putem să construim de exemplu
intersecția medianelor adică centrul
de greutate al triunghiului și
avem aici medianele acestui triunghi
punctul lor de intersecție adică
centrul de greutate coincide și
cu ortocentru și cu punctul de
intersecție al bisectoarelor dar
și cu centrul cercului circumscris
bazei pentru că repetă avem un
triunghi echilateral și să notăm
aici ca avem punctul o centrul
cercului circumscris bazei acum
în punctul o Pe planul abc vom
ridica o perpendiculară și pentru
aceasta so trasăm cu altă culoare
Deci ridicăm perpendiculara pe
planul abc o voi trasa punctat
pentru că ea va fi în interiorul
piramidei Deci nu se vede practică
așa cum nu se vede nici această
muchia bazei ace acum vom trece
aici vârful V adică vârful piramidei
și acum unim vârful piramidei cu
vârfurile bazei avem unun imp apoi
pe vecu b pardon bun și mai unim
pe V cu ce Dar Haideți să venim
mai bine așa și astfel am obținut
piramida V a ce să trec aici vârful
deasupra v o este de fapt înălțimea
acestei piramide înălțimea unei
piramide regulate este distanța
de la Vârful piramidei Da la centrul
cercului circumscris bazei V este
perpendiculară pe planul bazei
de ceai de să notăm că aici avem
înălțimea piramidei regulate am
numit o să construim acum apotema
piramidei Ce este apotema piramidei
este distanța de la Vârful piramidei
la o muchia bazei asta înseamnă
că trebuie să ducem perpendiculară
din b pe un muchia bazei ce idee
să ducem perpendiculară din vârful
piramidei pe muchia b c în primul
rând Ce reprezintă acest punct
Păi aceasta este mediană în triunghiul
ABC este semne că acest punct pe
care îl notăm m este de fapt mijlocul
segmentului b c avem că m c congruent
cu b e cu alte cuvinte dacă unim
pe V cu m si vom obține Păi avem
de fapt un mediană în triunghiul
v b c care este un triunghi isoscel
cu vârful în v Păi asta înseamnă
că vm este pe lângă mediană și
înălțime de ce avem aici un unghi
de 90 de grade pe asta înseamnă
că vm este distanța de la Vârful
piramidei la muchia bazei de ce
Deci vm este apotema în această
piramidă trecem aici că venea potema
piramidei care Atenție se notează
amic indice să construim acum apotema
bazei care Iată este distanța de
la centrul cercului circumscris
bazei la o muchie a bazei Deci
trebuie să ducem perpendiculară
din o să o ducem tot pe muchia
b c și vom găsi astfel apotema
bazei însă înainte Ce este a m
a m este mediană în triunghiul
echilateral ABC bun Păi asta înseamnă
ca imi este și înălțime punctele
a o și m sunt Cum sunt coliniare
înseamnă că om pe care Haide să
o trasăm om este perpendiculară
pe De ce Deci om reprezintă de
fapt apotema bazei trecem aici
om este apotema bazei care se notează
astfel a mic indice b și acum Haideți
să facem în așa fel încât să nu
se mai vadă medianele acestuia
acestă triunghi a b c pentru Oricum
ele trebuiau să fie trasate punctat
bun Și iată ce avem avem că v o
este înălțimea în piramida V a
b c d c v o e perpendiculară pe
planul bazei asta înseamnă că și
aici avem un unghi de 90 de grade
vor pendular automat și pe om mai
știi că vm este apotema piramidei
iar om este apotema bazei sigur
și om trebuia trasată punctat pentru
că este în interiorul piramidei
în să o lăsăm așa se vadă mai bine
ultima observație legată de notația
unei piramide triunghiulare regulate
cu asemenea piramidă nu o Vom numi
Oricum de exemplu piramida a b
c v și vom începe cu vârful deci
ia se numește piramida V a b c
începem întotdeauna cu vârful să
vedem acum desfășurarea unei piramide
triunghiulare regulate pentru această
apă sunt pe butonul de deschidere
bun aceasta este desfășurarea unei
piramide triunghiulare regulate
triunghiurile fețele laterale sunt
triunghiuri isoscele iar baza este
triunghi echilateral și acum so
închidem la loc