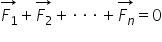Echilibrul de translație
În punct material se află în echlibru de translație dacă este în stare de repaus sau în mișcare rectilinie uniformă.
Dacă un punct material este în repaus sau mișcare rectilinie uniformă accelerația lui este nulă. Astfel putem afirma că, un punct material se află în stare de repaus sau de mișcare rectilinie uniformă dacă asupra lui nu acționează nici o forță sau dacă suma forțelor ce acționează asupra lui este egală cu zero.
Inexistența forțelor este echivalentă cu principiul inerției.
Dacă asupra punctului material acționează n forțe atunci:
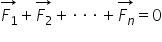
Deoarece discutăm despre un punct material, toate forțele ce acționează asupra lui sunt concurente.
Dacă asupra unui punct material acționează două forțe, punctul material este în echilibru de translație doar dacă forțele sunt egale în mărime, au aceeași direcție, dar sunt opuse ca sens.
Dacă asupra unui punct material acționează trei forțe, așa ca în figură:
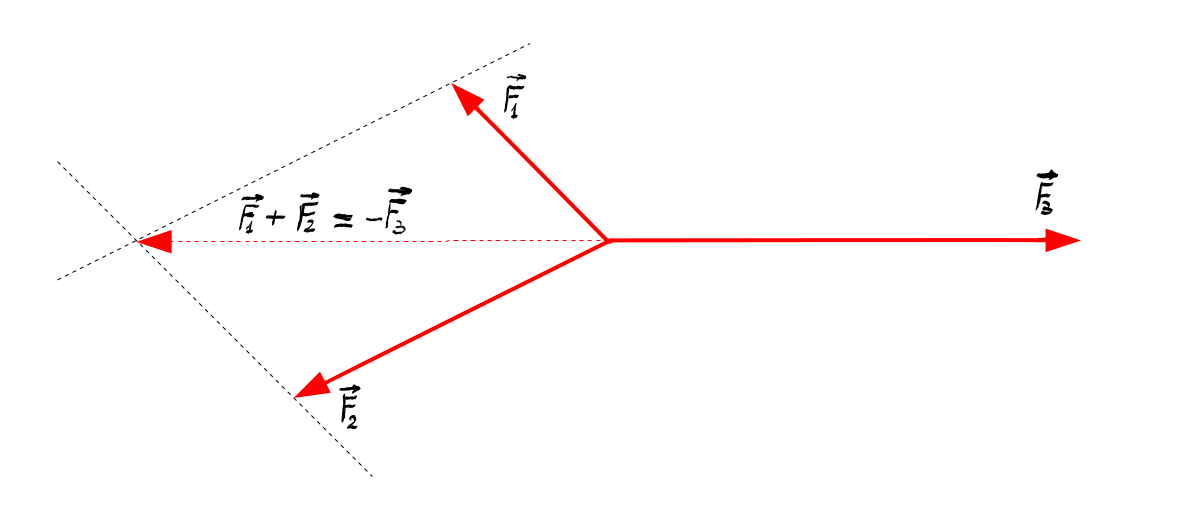
Atunci, pentru ca un punct material, acționat de trei forțe, să fie în echilibru de translație este necesar ca suma vectorială a oricăror două forțe să fie egală în mărime cu a treia forță, să aibă aceeași direcție cu cea de-a treia forță, dar să aibă sens opus cu cea de-a treia forță.
Dacă asupra unui punct material acționează mai multe forțe este utilă alegerea unui sistem de axe de coordonate convenabil, fixat de punctul material. Se descompun forțele după axele de coordonate. Echilibrul de translație este atins dacă suma vectorială a componentelor forțeor după axele de coordonate scrisă pentru fiecare axă de coordonate este egală cu zero.
Echilibrul punctului material supus la legături
Prin legătură înțelegem orice cauză care limitează mișcarea unui punct material. Firele inextensibile, firele elastice sau resorturile, suprafețele, pereții, etc. sunt considerate legături.
Fiecare legătură este caracterizată de o forță de legătură. Firele sunt caracterizate de forța de tensiune, resorturile de forța elastică, suprafețele de forța de reacțiune normală, etc.
Forțele de legătură se adaugă la suma vectorială a forțelor ce acționează asupra punctului material.
Condiția necesară și suficientă pentru ca un punct material să fie în echilibru de translație este ca suma vectorială a tuturor forțelor ce acționează asupra lui, inclusiv a forțelor de legătură, să fie nulă.