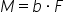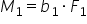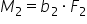Rotaţia solidului rigid. Momentul forţei. Cuplul de forţe.

începem doua lecție de statică

vom discuta despre momentul forței

și despre cupluri de forțe să discutăm

în înainte despre mișcarea de rotație

în jurul unei axe în lecția precedentă

de statică pentru studiul echilibrului

de translație am considerat puncte

materiale pentru a invita complicație

mișcării de rotație ce o impune

acțiunea forțelor externe Asupra

unui corp cu dimensiuni neglijabile

adică cu un volum acum Să considerăm

cazul opus și anume un corp cu

dimensiunile neglijabile fixat

pe o axă bineînțeles ce vom obținem

este o mișcare de rotație sub acțiunea

forțelor externe în jurul acestei

ax dar fără a avea și o mișcare

de translație datorită faptului

că corpul este fixat un exemplu

foarte simplu de astfel de corp

este o ușă Deci dacă acesta este

un perete și în punctul A avem

o ușă fixată în balamale Deci AB

este o ușă atunci dacă aplicăm

o forță f din anumit la anumită

mărime magnitudine obținem o rotație

în jurul axei care în cazul acesta

este perpendiculară pe ecran trecând

prin punctul am unde sunt balamalele

ușii Dar fără a avea și o translație

Deci o ții obținem o rotație a

ușii în jurul axei ce trece prin

punctul a un alt caz în interesant

ar fi dacă luăm aceeași ușă de

aceeași dimensiune prinsă în balamale

în punctul A pe ab de aceeași lungime

l dar în loc să aplicăm Forța F

la capătul b al ușii o aplicăm

mult mai aproape de balamale Deci

avem aceeași forță cu aceeași magnitudine

dar să zicem aplicată la o distanță

el pe patru un sfert din lățimea

ușii Ce observăm este că obținem

o mișcare de rotație dar ea este

mult mai încet în final să discutăm

un ultim caz Deci aceeași ușă de

aceeași dimensiune el Deci avem

Am lungimea uși fiind aceeași el

și aplicăm o forță de aceeași magnitudine

f dar perpendicular pe OX a ușii

Deci dealungul Forța F acționează

dealungul uși la Lungulețu și Ce

observăm că este că în acest caz

nu obținem nici o rotație în concluzie

rotație imprimată unui corp cu

dimensiune neglijabile depinde

atât de magnitudine forței aplicate

de distanța dintre forță și axul

de rotații dar și de orientare

a acestei forțe în concluzie introducem

așa numitul braț al forței Care

este distanța dintre dreapta suport

a forței și axa de rotație Deci

pentru fiecare caz consideră în

dreapta suport a forței și axuri

de rotații care din nou este perpendicular

pe ecranul dumneavoastră prin punctul

A și calculăm distanța dintre aceste

două drepte în cazul a brațul forței

să notăm cu d este el în cazul

al doilea să numim pe brațul forței

este lp4 distanța dintre dreapta

suport a forței și axul de rotație

în ultimul caz dreapta suport a

forței trece prin axul de rotație

Deci brațul forței este 0 vedem

că rotația Ea este proporțională

cu acest braț al forței în concluzie

introducem mărimea numită momentul

forței care descrie efectul de

rotație al unui corp sub acțiunea

unei forțe externe și ea este mărimea

vectorială cu modulul egal cu produsul

dintre forță și brațul forței Deci

va fi efort de a cărei direcție

este pe axa de rotație și semnul

ei va fi dat de sensul rotații

generate Haideți explicăm un pic

aceste lucruri Deci considerăm

un corp de dimensiuni oarecare

și formulare care și o axă ce trece

prin el pe care o notăm cu Delta

în care corpul este fixat Deci

corpul este fixat pentru o un mijloc

oarecare de a lungul axei Dalta

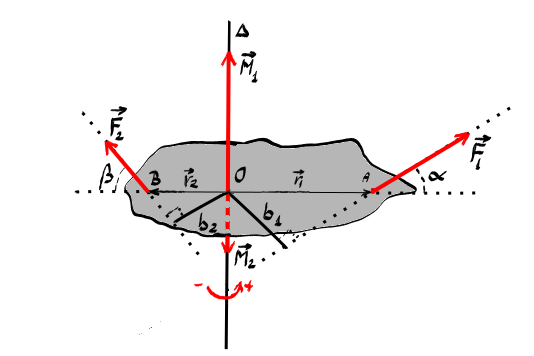
și aplicăm 1 o forță F1 ce avem

această forță F1 care are un pret

de 1 bineînțeles în acest caz momentul

forței m 1 al forței F1 va fi F1

de 1 considerăm un sens de rotație

pozitiv și stabilim semnul să momentului

forței în funcție de acest semn

convențional luat pozitiv Deci

față de acest sens pozitiv luat

momentul mm1 va fi pozitiv pentru

că rotația generată de Forța f1

va avea același sens după cum se

vede bineînțeles din figură pentru

a exemplifica mai departe să luăm

o forță F2 nici o forță F2 cambrat

de 2 vedem imediat că momentul

forței F2 va fi produsul dintre

doi și de doi brațul ei dar va

avea un semn negativ pentru că

rotația imprimată corpului de către

forța F2 este de sens opus sensului

pozitiv Deci cel mai important

lucru și veți vedea de ce în aceste

Două semne și generală în semnul

momentului forței este semnul relativ

al celor două momente sau a mai

multor momente în general pentru

că suntem interesați în suma acestor

momente de ce e important ca să

obținem semnul relativ între momentele

a doua Deci dacă prin Convenția

ONU este plus după aceea important

este Cum sunt celelalte momente

pozitive sau negative alte comentarii

importante carsi că dacă Forța

este paralelă cu axa de rotație

Delta obținem un moment egal cu

0 de asemeni după cum am specificat

în discuția precedentă despre rotația

ușii Dacă dreapta suport a forței

se intersectează cu axa de rotație

atunci din nou momentul generat

este 0 Deci trebuie să reținem

aceste două cazuri în care momentul

este întotdeauna 0 dreapta suport

a forței paralelă cu axa de rotație

sau se ce se intersectează cu axa

de rotație se numește cuplu de

forțe un sistem de două forțe paralele

de sens opus cu același modul Deci

f1 egal cu F2 notat cu F aplicată

acelui aceluiași corp Deci în cazul

acesta am avea sau Haide să desenăm

un nou corp pentru claritate Deci

dacă avem un corp și o axă de rotație

să notăm tocul de alta se numește

cuplu de forțe un sistem de două

forțe cu modulul egal dar cu sens

opus care acționează pentru eroti

corpul în jurul acestei axe se

numește brațul acestei acestei

acestui cuplu de forțe distanța

dintre dreptele suport a celor

două forțe se notează cu b momentul

cuplului notat cu MC va fi magnitudinea

uneia din cele două forțe egale

înmulțită cu brațul dintre cele

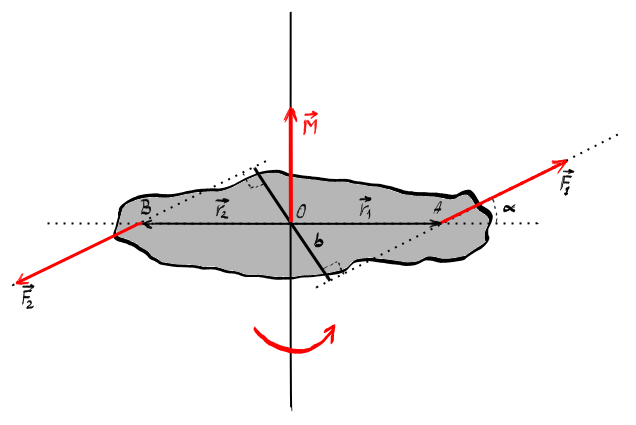
două forțe Haideți să rezolvăm

un exemplu de momente ale forțelor

aplicate unui corp de slime în

corp de dimensiune și formă oarecare

două puncte în în interiorul acestui

corp notate a și b și următoarele

forțe ce acționează asupra lui

R notăm cu l distanța dintre a

și b Ce sistem și avem următoarele

forțe în punctul A Forța f1 Care

este perpendiculară pe AB și o

forță F2 care face un unghi Alfa

cu ab în punctul B avem o forță

F 3 perpendiculară pe AB dar în

punctul b o forță F4 de a lungul

lui AB și o forță S5 care face

unui unghi Beta cu dreapta AB stabilim

un sens de rotație pozitiv prin

convenție acesta și știm Deci următoare

lucru că toate cele cinci forțe

F1 F2 f3 F4 și F5 se află în planul

ecranului nici în planul ecranului

știi magnitudine de lor F1 este

egal cu 10 newtoni S2 este egal

cu 15 RON iar 3 și f-4 Renault

Megane și egal cu 20 de Newton

și F5 10 minute cunoaștem De asemeni

unghiurile Alfa este egal cu 45

de grade Veta 30 de grade și distanța

dintre punctele a și b notate de

Noriel 10 cm Care notația științifică

este 10 la minus unu metri notația

științifică a fost descrisă în

prima lecție de cinematica avem

de asemenea două axe de rotații

o axă Delta notate cu Delta va

trece prin punctul A și perpendiculară

pe planul ecranului Deci Delta

este Prin a și perpendiculară pe

ecranul dumneavoastră Deci intru

în fel vine spre dumneavoastră

din ecran și o axă Delta prin care

trece prin punctul b și la fel

perpendiculară pe ecran și dorim

să calculăm momentele tuturor celor

cinci forțe față de cele două axe

Delta și Delta prin și momentele

totale să începem cu Axa Deltă

observând imediat că momentele

forțelor F1 F2 și F4 vor fi egal

cu zero pentru că dreptele suport

ale chestor forțe se intersectează

cu Delta în particular dreapta

suport a lui S4 este de al unghiului

ABD se va intersecta cu Delta le

vor avea brațe 0 Deci momentul

lor va fi zero momentului f1 egal

cu momentului S2 egal cu momentul

lui F4 Chic alicuza momentului

S3 față de Delta este egal cu minus

f3 ori el Deci is trei este perpendicular

pe AB Deci brațul ei este chiar

distanță a b l și sensul este negativ

pentru că mod Evident rotația generată

de S3 va fi în sens invers sensului

luat plin convenții ca pozitiv

Deci ea este negativ și obținem

calculând minus 2 Newton ori metru

momentul forței f 5 singura care

a rămas de calculat față de Delta

va fi egal cu plus F5 sinus de

beton să vedem de ce Deci pentru

a calcula brațul acestei forțe

luăm dreapta suport a lui S5 și

calculăm distanța față de dreapta

Deci acest unghi este de 90 de

grade Acesta este un ghiul beton

și Deci dreapta suport va fi să

notăm cu a c Nici acesta este accepta

suportă brațul forței scuzați brațul

forței 5ac Care este sinus de b

a c calculând obținem Plus 10 ori

10 la minus 1 sinus de 30 de grade

Adi când plus 0 Newton ori acum

suntem gata să calculăm momentul

total față de axa Delta Care este

suma algebrică al tuturor momentelor

celor cinci momente ale celor cinci

forțe obținem că acest moment față

de Delta este negativ și egal cu

minus 1 Newton ori metru în concluzie

față de axa Delta avem o mișcare

o rotație în sens contrar sensului

va prin convenții pozitiv și acum

vedem de ce este important semnul

relativ al acestor momente ale

forțelor nu contează în ce sens

alegem Convenția atât timp cât

avem semnele relative corecte Pentru

că atunci vom obține semnul final

corect față de Convenția alea sunt

și deci putem stabili fără echivoc

sensul rotații în acest sens opus

sensului pozitiv la prin convecție

cel de al doilea caz este rotația

față de axa Delta prin iarăși față

de Delta prin momentele forțelor

F 3 f-4 65 vor fi 0 motivele fiind

evidente au brațul 0 Deci momentul

3 egal cu momentul lui F4 egal

cu momentul lui S5 egal cu 0 momentul

lui F1 va fi egal cu minus 1 ori

minus pentru că din nou mod Evident

F1 va imprima o rotație în sens

opus sensului pozitiv Deci notația

lui F1 va fi așa se supără Steve

este invers Deci semn semnul este

negativ față de funie este el Deci

minus 10 ori 10 la minus 1 care

înseamnă că avem un moment total

din minus un Newton ori metru momentul

forței doine față de Delta prim

este egal cu plus F 2 înmulțit

cu el sinus de aur de ce Pentru

că trebuie să calculăm brațul forței

doi Deci Considerăm daca suporta

lui ostoi și apoi calculăm distanța

ei față de Delta prima aceasta

va fi segmentul de Sănătate tu

la sesta cu de Deci brațul forței

2 față de Delta prin este bendy

iar b d este al sinus de Alfa acest

unghi este de 90 de grade Deci

obținem Plus 15 ori 10 la minus

1 ori sinus de 45 de grade Deci

în total plus 1 Newton ori metru

făcând suma algebrică a tuturor

acestor momente ale forțelor obține

încă momentul total față de axa

Delta prime este egal cu plus 0

ori Metro Deci momentul total al

tuturor forțelor față de axa Delta

prim Este pozitiv Deci față de

axa Delta prin Forțele vor genera

o rotație în sensul pozitiv există

multe aplicații practice ale momentelor

forțelor sau cuplurilor de forțe

un exemplu foarte simplu este o

cheie care înșurubează o piuliță

ia mod Evident va folosi un moment

al forței aplicată la capătul cheie