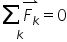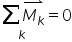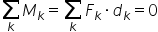Legea echilibrului de rotaţie. Stabilitatea echilibrului.

În ce an a treia lecție de statică

vom discuta despre echilibrul de

rotație și despre noțiunea de stabilitate

a echilibrului echilibru de rotație

a unui corp solid ce se poate roti

in jurul unei axe se obține sub

acțiunea unor forțe dacă suma algebrică

a momentelor forțelor în raport

cu acea axa este nulă acest concept

de suma algebrică a momentelor

forțelor față de o axă a fost discutat

în lecția precedentă și înseamnă

pur și simplu că acest produs f

ori de care este momentul unei

forțe are un semn plus sau minus

stabili pentru anumită convenție

Și acel semn este luat în calcul

Când se face suma momentelor forțelor

datorită faptului că acești produși

poți pozitiv sau negativ momentul

total poate fi 0 și dacă este 0

atunci obținem echilibrul de rotație

vă invit să recapitulat lecția

trecută unde dăm și noi exemplu

de calcul dar foarte pe scurt dacă

avem o axă de rotație care sunt

notat cu Delta și două forțe F1

Spre exemplu și F2 atunci în mod

Evident F1 va genera o rotație

întrun sensului prin convenție

pozitiv al corpului în timp ce

f2a va genera o rotație în sensul

opus În consecință momentul forței

F2 va fi negativ dacă suma algebrică

ce ține cont de acest semn a celor

două forțe este 0 atunci obținem

un echilibru de rotație al corpului

în jurul axei Delta să rezolvăm

un un exemplu simplu de echilibrat

rotație avem o tijă de lungime

l articulată întru un punct A de

un perete Deci avem un perete un

punct A și o tijă de lungime l

acționăm asupra ei cu o forță F1

orizontală și dorim să stabilim

unghiul Alfa cu peretele pentru

care această tijă se află în echilibru

de rotație Deci ca să recapitulăm

cunoaștem greutatea tijei Care

este 10 Newton cunoaștem Forța

f1 Care este 3 newtoni și este

orizontală și dorim să calculăm

unghiul Alfa pentru care se obține

un echilibru de rotație în jurul

axei ce trece prin a desenam întâi

Forțele de ce avem Forța f1 avem

apoi forța de greutate atinge și

mai există și o forță de reacțiune

a peretelui Care este perpendicular

pe suprafața peretelui să calculăm

momentele celor trei forțe momentul

față de ei a lui r a forței de

reacțiune este 0 pentru că ar trece

prin ei are brațe dar momentul

forței de greutate este egală cu

este egal cu minus gem brațul pe

care îl notăm cu A al forței să

explicăm Deci întâi Considerăm

prin convenție un sens pozitiv

de rotație și în mod Evident greutatea

va roti tija în sens opus acestui

semn luați prin convenție deci

de aceea momentului ce va fi negativ

brațul forței f g este distanța

dintre dreapta suport a greutății

și axa de rotație Ce este perpendiculară

pe ecranul dumneavoastră trecând

prin și Deci acest a h este dreapta

este brațul forței G Deci avem

că momentul lui G este minus gem

înmulțit cu el pe 2 sinus de elf

pentru că distanța dintre A și

punctul de aplicație al forței

să notăm cu ce Deci AC este el

pe 2 și Deci acesta este alcătuit

și Deci Aha va fi el pe 2 sinus

de Alfa momentul forței F1 este

egal cu plus f-1 înmulțit cu deca

pardon nu cu ei ca deci F1 are

această dreaptă suport și atunci

brațul ei este a ca unde ca este

punctul de intersecție dintre prelungire

a forței și Deci înmulțit cu ei

ca sensul este pozitiv Doarece

în mod Evident F1 va genera o rotație

în același sens cu sensul luate

prin convenții pozitiv Deci obținem

că momentul forței F1 este plus

F1 mulți cu el cosinus Steaua deci

acum este el lungimea tijei ori

cosinus de Alfa Pentru că așa este

cateta alăturată obținem că momentul

total Care este suma algebrică

a tuturor acestor momente Deci

momentul este egal cu minus g l

pe 2 Sin Alpha plus F1 car dar

știm că Iza se află în echilibru

de rotație echilibru de rotație

ceea ce înseamnă că acest moment

total este egal cu 0 din aceasta

scoate ne crois ția că G Help 2

Sin Alfa este egal cu F 1 L coastal

Farm și Deci tangentă Da Alfa este

egal cu 2 F 1 împărțit Age putem

înlocui valorile numerice și obținem

că avem motan Un valoarea lui tangent

de Alfa de 0 ceea ce înseamnă că

unghiul Alfa la care se obține

echilibru de rotație este de 31

de grade să discutăm acum despre

noțiunea de stabilitate a echilibrului

am văzut că obținem echilibru de

translație când rezultanta forțelor

externe este zero Am discutat despre

acest lucru în prima lecție de

statică și că obținem un echilibru

de rotație când momentul total

al tuturor forțelor externe este

0 am discutat despre acest lucru

în cea de a doua lecție de statică

și începutul acestei lecții dar

întrebarea care se pune este Când

acest echilibru este stabil Ce

înțelegem prin noțiunea de stabilitate

un echilibru este stabil atât un

echilibru de translație cât și

de rotație dacă el rămâne un echilibru

și după încetarea acțiunii forțelor

inverse echilibru se numește instabil

în mod Evident dacă avem un echilibru

de translație sau urșii rotație

sub acțiunea unor forțe dar odată

ce îndepărtăm aceste forțe echilibrul

dispare se dă un exemplu simplu

avem o suprafață curbată și Avem

două Considerăm două corpuri pe

această suprafață două bile o bilă

pe fundul suprafețe în punctul

cel mai de jos și o bilă undeva

mai sus amândouă bilele se află

sub acțiunea gravitației Deci vor

avea o greutate G Să presupunem

că amândouă sunt în echilibru Adică

că atât punctul A cât și punctul

B nu se mișcă nu au nici nici mișcare

de translație nici de rotație în

cazul punctului b asta presupune

acțiunea unei forțe externe care

să echilibreze componenta greutății

tangențiale la suprafața care ar

face corpul să cadă spre interiorul

suprafeței Deci presupunem că avem

Care este egal cu g tangențială

în acest caz și bila de va fi in

echilibru acum întrebarea ce se

pune este Ce se întâmplă cu bila

B1 dacă îndepărtăm forța aer în

mod evident starea de echilibru

va dispare și anume Billa va intra

între o mișcare de translație accelerată

și Deci acest echilibru este un

echilibru instabil dispare ce se

întâmplă cu bila a dacă îi aplicăm

o forță f egal observăm că ea intră

între o mișcare de translație dar

că o dat o dată ce îndepărtăm Forța

F ia se va așeza după o mișcare

de o anumită perioadă în același

punct în aceeași poziție de echilibru

Concluzia este că bila din poziția

b care inițial se afla în echilibru

datorită acțiunii forței Iași este

întruni echilibru instabil pentru

că din nou odată ce ieftin spare

echilibru dispare și el invers

bila din Billa a din această poziție

se află întrun echilibru stabil

odată îndepărtată Forța F care

perturbă în acest caz poziția de

echilibru inițială ia tinde să

revin în această poziție de echilibru

Deci Tiki libru din această poziție

este un echilibru stabil în general

se conectează noțiunea sau conceptul

de echilibru stabil cu acela de

energie potențială minimă pentru

că observăm că între Toate aceste

poziții de a lungul suprafeței

de var e înălțime H față de Pământ

de aceasta este pământul singura

poziție care are un echilibru stabil

este cea din cu înălțime minimă

din poziția am toate celelalte

poziții sunt instabile au echilibru

instabil Deci echilibrul stabil

se obține când energia potențială

care în acest caz este m g h este

minimă acest lucru este valabil

și pentru alte tipuri de energii

potențiale această echivalență

între echilibru stabil și energie

potențială minim de exemplu și

pentru energie potențială elastică

și așa mai departe