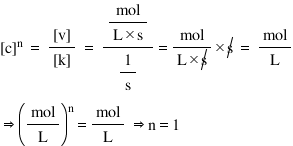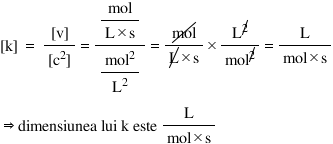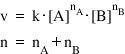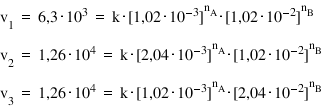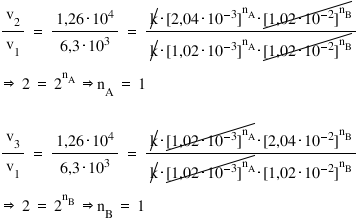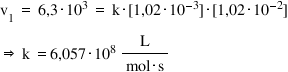Timpul de înjumătăţire, t1/2, reprezintă timpul necesar pentru ca jumătate din cantitatea iniţială de reactant să reacţioneze. Expresia matematică care ţine cont de faptul că acum avem jumătate din concentraţia iniţială de reactant, este următoarea:
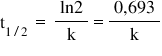
Pentru o reacţie cu ecuaţia generală:
aA 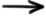 produşi de reacţie
produşi de reacţie
şi cu expresia vitezei de reacţie de această formă: v = k·[A]n
avem tabelul de mai jos cu date despre reacţiile cu această formă generală. Reacţiile chimice care au acelaşi ordin de reacţie au anumite caracteristici comune.
|
Ordinul de reacţie
|
Legea vitezei de reacţie
|
Raportul v2/v1, unde:
v1: c1
v2: c2 = 2c1
|
Unitatea de măsură pentru k
|
|
n = 0
|
v = k
|
v2/v1 = 1, deci v nu depinde de c
|
mol/L·s
|
|
n = 1
|
v = k·[A]
|
v2/v1 = 2, deci dublarea concentraţiei reactantului duce la dublarea vitezei de reacţie
|
s-1
|
|
n = 2
|
v = k·[A]2
|
v2/v1 = 4, deci la dublarea concentraţiei reactantului, viteza de reacţie creşte de 4 ori
|
L/mol·s
|
1. În unele probleme de calcul nu cunoaştem ordinul de reacţie, însă ni se dă dimensiunea constantei de viteză. Astfel, putem deduce singuri ordinul de reacţie.
Avem legea vitezei de reacţie în forma de mai jos, şi ni se dă unitatea de măsura pentru k: s-1. Trebuie să aflăm ordinul de reacţie, n.
v = k·cn
- ştim că unitatea de măsură pentru viteză este mol/ L·s, iar unitatea de măsură pentru concentraţie este mol/L.
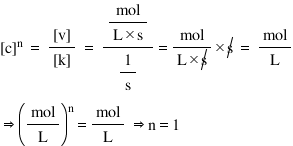
2. Este la fel de simplu să aflăm dimensiunea lui k în cazul în care cunoaştem ordinul de reacţie.
Avem următoarea expresie a vitezei de reacţie a unei reacţii oarecare:
v = k · c2
- cunoaştem unităţile de măsură pentru viteză şi concentraţie.
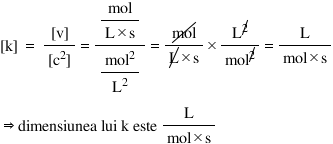
3. Pentru o reacţie chimică ce are loc între doi reactanţi s-au făcut trei experimente cu diferite concentraţii de reactant A şi B.
aA + bB  produşi de reacţie
produşi de reacţie
Tabelul de mai jos redă variaţia vitezei în funcţie de concentraţia reactanţilor:
|
|
v (mol/L·s)
|
A (mol/L)
|
B (mol/L)
|
|
Experiment 1
|
6,3 · 103
|
1,02 · 10-3
|
1,02 · 10-2
|
|
Experiment 2
|
1,26 · 104
|
2,04 · 10-3
|
1,02 · 10-2
|
|
Experiment 3
|
1,26 · 104
|
1,02 · 10-3
|
2,04 · 10-2
|
- care este ordinul total de reacţie, n?
- care este valoarea constantei de reacţie, k?
Expresia matematică a vitezei de reacţie:
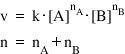
Înlocuim datele experimentale în expresia matematică a vitezei de reacţie:
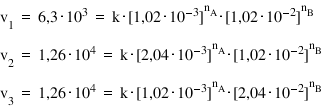
Pentru a afla ordinele parţiale de reacţie, ne putem folosi de rapoarte între vitezele de reacţie:
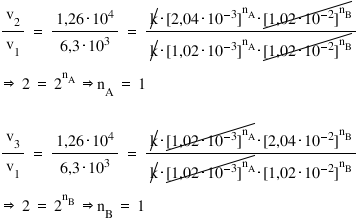
Aşadar, ordinul total de reacţie este n = 2
Pentru calculul constantei de viteză k, înlocuim datele într-una dintre expresiile matematice ale vitezei, spre exemplu v1:
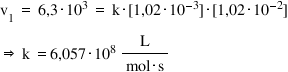

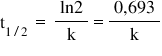
 produşi de reacţie
produşi de reacţie