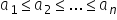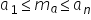Media aritmetică a două sau mai multe fracții (numere) zecimale finite

să facem acum câteva exerciții

cu media aritmetică a două sau

mai multe fracții zecimale finite

însă înainte de aceasta Ce semnifică

media aritmetică media aritmetică

exprimă un nivel mediu o valoare

medie de exemplu dacă avem un grup

de alpiniști care doresc să escaladeze

un munte sport să ajungă în vârful

acestui munte și sau hotărât să

le Scala des în patru zile astfel

în prima zi până la primul popas

vor parcurge de la baza 3 km apoi

de la primul popas până la următorul

în a doua zi adică parcurs 5 km

apoi 4 de km și în final 7 km înainte

de a pleca la drum a se întreabă

Care este distanța medie pe care

o au de parcurs Păi pentru aceasta

iei Adună toate aceste distanțe

astfel avem 3 adunat cu 5 adunat

cu 4 De ce aveam aici adunat cu

7 iar această sumă o împart la

câte distanțe au pe Câte numere

avem un au un număr două trei patru

avem patru numere am scris formula

pentru determinarea mediei aritmetice

acum media aritmetică Cu cât este

egală facem calculul Deci trebuie

să facem această sumă să notăm

aici avem 3 adunat cu 5 adunat cu

4 adunat cu 7 acum completăm aici

cu de un zero ca să avem două zecimale

că aici și pe șapte scriem 7 și

suma obținem aici 6 aici avem unul

cu u67 cu doi nouă coborâm virgula

trei cu cinci opt cu 412 cu 719

Deci obținem 19 împărțit la patru

apoi Haide să ștergem și să facem

și împărțirea 19 împărțit la 4 și

avem 19 împărțit la 4 4 4 x 4 16

facem diferența obținem 3 am ajuns

în dreptul virgulei o trecem la

cât Și coborâm următoarea cifră

a adică 9 4 intră în 39 de 9 ori

9 ori 4 ne dă 36 facem diferența

obținem 3 coborâm pe 6 36 împărțit

la patru nouă nouă 436 și sa încheiat

împărțirea Deci avem 4 zeci și nouă

valoarea mediei aritmetice acum

am spus că media aritmetică reprezintă

o valoare medie să știți că întotdeauna

media aritmetică Cum e în cazul

nostru 4 această valoare este cuprinsă

între cel mai mic și cel mai mare

dintre numerele date Ia 4 este mai

mare sau egal cu 3 și mai mic sau

egal cu 7 întotdeauna avem această

egalitate să pardon avem această

relație putem spunem și că media

aritmetică exprima tendința centrală

a unui șir de numere astfel Haide

să ștergem aici dacă trece acest

șir de numere și scrie numerele

în ordine crescătoare Deci mai

întâi avem 3 apoi avem 4 apoi avem

5 și apoi îl avem pe 7 Media aritmetică

pe care am obținut o este 4 pe Ce

observăm că media aritmetică este

cuprinsă între aceste două numere

care se află în mijloc de aceea

spunem că arată o tendință centrală

a acestui șir de numere însă din

curiozitate vă pot spune că nu

pentru toate șirurile de numere

media aritmetică exprima tendința

centrală a șirului respectiv De

exemplu dacă valorile sunt foarte

distanțate să spunem că avem deci

punem aici un Semn de exclamare

avem aceste valori trei 4 și următoarea

valoare este 100 atunci media aritmetică

va fi situat undeva între aceste

două numere e de fapt 28 și ceva

Deci în această situație în care

numele sunt foarte distanțate media

aritmetică nu este folosită ca

să exprime o tendință centrală

a unui șir de numere însă când

avem numere mai apropiate ca aici

atunci media aritmetică a folosită

pentru acest lucru Haideți să facem

acum câteva probleme să spunem

că în urmă A4 test la care am luat

aceste note 7 610 am învățat mai

bine Și 8 deci să spunem că în urmă

a numai notelor luate la aceste

patru teste se va trece un opt

în catalog Cum aflu ce notă voi

primi în catalog Păi pentru a calcula

nota pe care o voi primi și cred

că sunteți obișnuiți se face media

aritmetică a numerelor de aici

Deci mai întâi adunăm cele patru

numere iar suma o Vom împărți la

câte numere avem 1 2 3 4 4 numere

ceai de să calculăm valoarea mediei

aritmetice zecile adunăm mai întâi

7 adunat cu 6 adunat cu Z și cu

8 mai ales să completăm is trecem

virgulă și un zero la fel și aici

și în sumă 3 cu 7 10 Deci 0 și

1 în minte avem aici 7 cu 613 cu

1023 cu 831 cu unul din minte 32

Deci Avem 32 32 împărțit la 4 cu

alte cuvinte obțin voi primi în

catalogul nota opt Acum putem să

facem și in verificările în sensul

că media aritmetică a Dică valoarea

opt observăm că este cuprinsă între

cel mai mic și cel mai mare dintre

numere este cel mai mic este 6

și cel mai mare este 10 6 este

mai mic sau egal cu 8 și 8 este

mai mic sau egal cu 10 tot așa

Putem să evidențiem și faptul că

media aritmetică exprimă tendința

centrală a acestui șir de numere

dacă scriem numerele în ordine

crescătoare Deci avem aici 6 apoi

7 8 și 10 Ce observăm media aritmetică

este 8 Adică este situată între

aceste două numere de ceartă Că

întradevăr numerele fiind suficient

de apropiate atunci media aritmetică

exprima tendința centrală a acestui

șir alt exemplu pe să spunem că

vreau să măresc media la istorie

și doamna sa profesorul mie a spus

că am două note iar media lor este

8 Deci am două note cu media aritmetică

egală cu 8 Ce notă ar trebui să

iau astfel încât să măresc media

Păi Haideți să ne gândim puțin

ca să pot să calculez în noua medie

pe care aș pe care aș putea să

o obțin trebuie neapărat Să știm

și notele pe care le am deja practica

să aflu noua medie ca să o pot

calcula trebuie să am cele două

note Haide să le prezentăm prin

aceste două cercuri am aceste două

note dar nu știu care sunt și mai

am nevoie de noua notă pe care

o voi obține ca să calculez media

lor trebuie să le aduni iar rezultatul

îl împart la câte note am în total

adică unu doi trei Da trei note

și voi obține noua medie aritmetică

acum ca să fac acest calcul am

neapărat nevoie de valorile acestor

două note de fapt ce îmi trebuie

îmi trebuie suma lor Păi tem să

aflăm suma lor sigur atunci când

ni se dă numărul de note și știu

și media lor aritmetică putem să

aflăm suma notelor respective astfel

știind că adunând cele două note

și împărțind la 2:00 pentru că

avem două nu se obține media lor

aritmetica adică ne dă 8 alte cuvinte

suma lor să mutăm așa este egal

cu este egală cu 8 ori 2 adică

16 Deci am de terminat valoarea

acestei sume atunci putem să venim

și să înlocuim această sumă o Vom

înlocui aici cu numărul 16 Deci

Haide să notăm avem 16 adunat cu

nota pe care o voi obține totul

împărțit la trei și acum Ce notă

ar trebui să obțin ca să măresc

media să nu mai am media 8 Păi

dacă aș obține dar exemplu nota

10 atunci vom avea 16 cu 1026 împărțite

la 3 să vedem cât ne dă 26 împărțit

la trei opt ori 324 obține Maicii

2 adăugăm un 01a de spațiu să scriem

în să trecem virgula la cât Și

coborâm în zero aici 20 împărțit

la 3 6 6 ori 318 din nou obținem

2 din 9 adăugăm 0 iar și vom avea

șase șase ori 318 din 9 2 și așa

mai departe De fapt avem 8 de să

notăm 8 păi prin rotunjire acest

număr ne va da media nouă Deci

obținem media90 Namur imediat de

la 8:00 la 9:00 Dar oare e neapărat

nevoie să luăm mă să iau nota 10

Dacă aș lua nota 9 atunci 16 plus

9 împărțit la trei înseamnă 25

împărțit la trei și facem acum

împărțirea 25 împărțit la trei

doi opt ori 3 ne dă 24 obținem

aici unu coborâm zero și să trecem

și virgulă 10 împărțit la trei

trei trei ori trei nouă iar și

obținem aici 1 și așa mai departe

De fapt o să obținem 8 asta înseamnă

că de fapt vom rămâne cu media

8 finul mare ca să îmi măresc media

Trebuie neapărat să iau Bia să

iau aici și nota 10 și acum idee

să facem o problemă clasică media

aritmetică a trei numere este 10

Două dintre ele sunt 2 și 5 Care

este al treilea număr știind că

avem trei numere iar media lor

aritmetică este 10 cunoaștem deja

două dintre numere Deci avem 2 și

5 pe al treilea număr pe care vrem

să îl aflăm Haideți să notăm cu

x pentru a nota media lor aritmetică

trebuie să adunăm aceste trei numere

iar suma să o împărțim la Câte

numere sunt adică la trei și știind

că obținem 10 atât este media aritmetică

cum determinăm valoarea lui x Păi

mai întâi putem să facem suma de

aici din paranteză avem 2 cu 5 înseamnă

8 adunat cu x totul împărțit la

3 ne dă 10 Păi determinăm această

sumă 8 plus x Cu cât este egal pe

Ce număr împărțit la 3 ne dă 10

foarte simplu 10 ori 3 suma 8 plus

x este egală de fapt cu 30 și acum

ca să îl găsim pachete foarte simplu

avem 30 minus 8 și facem diferența

vom obține 21
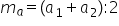
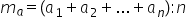