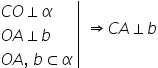Teorema celor trei perpendiculare

știind că atunci când Reprezentăm

în plan un corp psihometric Cum

este acest cub măsurile unghiurilor

nu se păstrează Iată măsura unghiului

d a b este de 90 de grade Deci

avem aici un unghi drept deși pe

desen pare că este un unghi ascuțit

sau alt exemplu unghiul a prim

d c adică acest unghi este tot

un unghi drept deși pe desen pare

obtuz la fel se întâmplă și cu

unghiul c prim de ei iată mă refer

la acest unghi tot așa este un

unghi de cu are are măsura de 90

de grade de ce avem aici 90 de

grade și unghiul c b a are 90 de

grade dar și c prim b a are 90

de grade însă aceste lucruri sunt

evidente pe desen pentru că în

plan un corp geometric atunci cum

putem să identificăm pe un asemenea

desen unghiurile drepte pentru

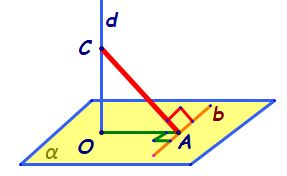
aceasta Folosind teorema celor

trei perpendiculare care ne spune

că dacă avem o dreaptă perpendiculară

pe un plan iar dreapta d este perpendiculară

pe planul alfa și o să luăm pe

dreapta d încă un punct o să avem

nevoie de el să îi spunem ce Deci

dacă avem o dreaptă perpendiculară

pe un plan și prin punctul de intersecție

al dreptei cu planul Deci prin

punctul O trece o altă dreaptă

care la rândul ei este perpendiculară

pe o dreaptă din plan să o notăm

această dreaptă cu b această dreaptă

să trecem punctul de intersecție

a Deci dreapta o a e perpendicular

pe b trec aici ca avem 90 de grade

atunci dreapta c a este perpendiculară

pe dreapta b mic de ce avem aici

90 de grade și chiar o să trasezi

această dreaptă si acum creion

mai gros se vadă mai bine prin

urmare ce ne spune teorema celor

trei perpendiculare ne spune că

dacă avem o dreaptă perpendiculară

pe un plan Deci dreapta c o sau

dreapta d este perpendiculară pe

planul alfa și dreapta o a perpendiculară

la rândul ei pe dreapta b mic dreptele

o a și b unde sunt sunt incluse

în planul alfa atunci din teoremă

celor trei perpendiculare voi scrie

așa și chiar să fac un rezultă

mai mare rezultă că c a este perpendiculară

pe b e ușor de înțeles De ce se

numește teoremă celor trei perpendiculare

pentru ca avem o perpendiculară

două și încă una Deci trei perpendiculare

Cum demonstrăm această teoremă

să trecem aici demonstrație Deci

trebuie să arătăm că ce a este

perpendiculară pe dreapta b mic

atâta timp cât știm să vedem ce

cunoaștem Păi știm că c o este

perpendiculară pe Alfa punctul

C nu aparține planului Alfa însă

punctul O aparține acestui plan

si mai cunoaștem o a este perpendiculară

pe dreapta b mic și cele două drepte

a și b Deci o a și b sunt inclusă

în acest plan alfa cu toate aceste

informații trebuie să arătăm că

ce ai perpendiculară pe b vă las

puțin timp să vă gândiți ca Să

arătăm că dreapta b este perpendiculară

pe dreapta c a vom arăta că dreapta

b perpendiculară pe planul c o

a dacă arătăm acest lucru atunci

cum dreapta cheia în clasă în acest

plan înseamnă că dreapta b este

perpendiculară și pe dreapta c

a pentru că repete perpendiculară

pe acesta plan cum arătam faptul

că dreapta b e perpendiculară pe

planul a o c sau co A păi trebuie

să găsim în acest plan două drepte

concurente și dreapta b să fie

perpendiculară pe fiecare din cele

două drepte în parte și deja avem

o dreaptă o dreapta b perpendiculară

pe o a și ne mai trebuie încă o

dreaptă concurentă cu o a Păi cum

sunt dreptele c o și b sunt perpendiculare

pentru că c o a perpendiculară

pe acest plan Deci venim și notăm

ce o perpendiculară pe planul alfa

dreapta b este inclusă în Alfa

Iată se vede și pe desenul observăm

și aici rezultă că dreapta c este

perpendiculară pe dreapta b sau

dacă vreți pot să scriu chiar invers

dreapta b perpendiculară pe c o

un avem că dreapta b perpendiculară

pe c o dreapta b e perpendiculară

pe o a știind din ipoteză Deci

b perpendiculară pe cele două drepte

c o și o a sunt drepte concurente

care punctul lor de intersecție

c o și o A punctul O rezultă că

dreapta a b perpendiculară pe planul

determinat de dreptele c o și o

A deci dreapta b mic perpendiculară

pe planul să facem aici perpendiculară

pe planul determinat de dreptele

c o și o a adică dreapta b mic

a perpendiculară pe planul c o

a însă acest plan conține dreapta

AC Deci dreapta si ei sau AC este

inclusă în planul c o a de unde

rezultă că avem o dreaptă perpendiculară

pe un plan înseamnă că dreapta

b perpendiculară pe orice dreapta

din plan de C perpendiculară și

pe cea dreapta b mic perpendiculară

pe c a și sa încheiat exact ce

voiam să arătăm că dreapta c a

e perpendiculară pe dreapta b să

revenim acum la primul nostru exemplu

și anume la cubul a b c d a prim

b prim c prim D prim Cum arătăm

că unghiul a prim b c are întradevăr

90 de grade poiată avem aici a

prim a Care este perpendicular

pe planul a b c d mai avem că AD

este perpendiculară pe BC avem

aici un unghi de 90 de grade atunci

conform teoremei celor trei perpendiculare

înseamnă că a prim d este perpendiculară

pe d c d ce avem aici 90 de grade

Haide să notăm deci a prim a perpendiculară

pe planul a b c d mai știm că AD

este perpendiculară pe BC a d și

d c sunt incluse în planul a b

c d atunci rezultă din teoremă

celor trei perpendiculare că a

prim d este perpendiculară pe DC

și astfel putem Să arătăm sau putem

să verificăm dacă întradevăr Un

unghi are măsura de 90 de grade