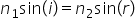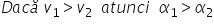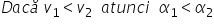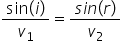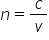Anexă: discuţie despre legea a doua a refracţiei.
Tag-uri
Partajeaza in Google Classroom

Transcript
în această anexă la prima lecție
de optică geometrică vei prezenta
mai detaliat cea de a doua lege
refracție reamintesc câteva noțiuni
discutate în acea lecție și pentru
aceasta voi desena o schemă care
se reamintească legea are fracții
și elementele necesare introducere
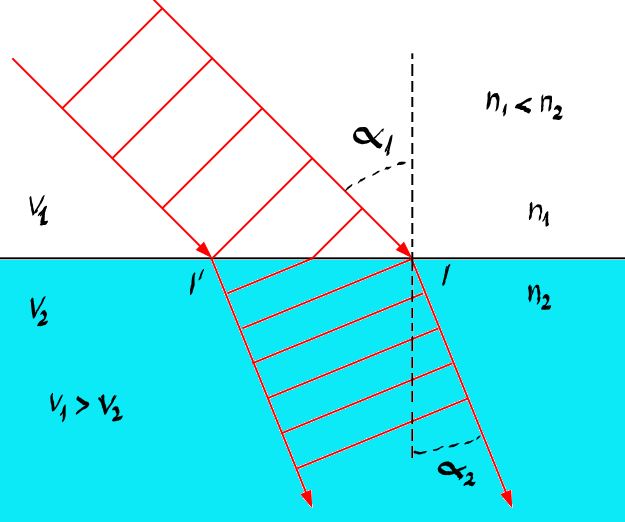
A deci avem o rază incidenta pe
suprafața de separare a două medii
omogene care au indicii de refracție
n1 și N2 aceasta întâlnește suprafață
de separare între un punct de incidență
iar această dreaptă este normală
la suprafață de separare în acel
punct în acest punct raza incidență
se separă în două raze o rază reflectată
și una refractat raza reflectată
se va propaga în noul mediu la
un nunți față de normală masca
față De separare notat cu a 2 unghiul
față de normală a razei incidente
era notat cu a și atunci ala două
la Legea refractiei era in 1 sinus
de e este egal cu n 2 sinus de
r2 pentru ei am dau explicații
intuitivă acestei legi să extindem
puțin modelul razei de lumină prin
Optica geometrică unde vă reamintesc
raza de lumina era o dreaptă în
sensul că acest aceasta va avea
o grosime ceea ce întotdeauna se
întâmplă realitate chiar și pentru
raze ca rază laser și se deplasează
și lumina se deplasează în interior
sub forma unor unde de viteză constantă
Deci extensia simplă a aceste raze
de lumină va duce la următorul
desen echivalent De ce raza inch
Sante va avea o grosime Deci va
fi mai degrabă ceva de genul acesta
va avea o grosime iar lumina se
propagă în interior sub forma unor
unde plane care se propagă cu viteză
constantă Deci aceasta este vectorul
viteză a luminii care are valoarea
1 în mediul 1 unghiul de incidență
vom muta un pic diferit și anume
alfa-1 veți vedea imediat De ce
Deci aceasta este extensia raza
incidența era numită grosime în
un lumina se propagă cu viteză
constantă sub forma acestora unde
și unghiul unghiul de incidență
este Alpha 1 Să considerăm cazul
în care primul mediu are o viteză
de propagare a luminii mai mare
decât cel de al doilea Merge deci
V1 mai mare decât V2 de 2 este
viteza de propagare în cel de al
doilea meci ce se întâmplă în momentul
în care lumina ajunge la suprafață
de separare este că primul punct
care ajungem va avea dintre odată
o viteză mai mică decât toate celelalte
puncte Da pentru că toate celelalte
puncte au viteza egală cu unu se
află în continuare în primul mediu
dar primul punct acesta de a trece
în cel de al doilea mediu care
are viteză mai mică De ce îl va
avea o viteză mai mică rând pe
rând toate punctele vor trece și
vor avea rând pe rând o viteză
mai mic și egal cu v2 Deci se observă
imediat că ce se întâmplă cu rază
de lumină este că ea se va întoarce
către stâng datorită acestui fenomen
că punctele își văd viteza micșorată
de la valoarea de 1 la valoarea
pe 2 mai mică unul câte unul Da
Și atunci ce se va întâmpla cu
raza în întregime este că va deveni
mai apropiată de normal Da deci
unghiul Alfa 2 L razei refractate
va fi mai mic decât alfa-1 Deci
în cazul în care vei Unul este
mai mare decât V2 alfa-1 este mai
mare decât alpha2 se poate vedea
imediat că în celălalt caz în ca
și anume cel în care vei Unul este
mai mic decât V2 se întâmplă să
nu meniul invers și anume primul
punct care ajunge la suprafață
de separare și care face primul
tranziția dintre viteza v1 și viteza
V2 va avea Din contră o viteză
dintre odată mai mare decât celelalte
puncte și și așa mai departe celelalte
puncte trec rând pe rând la o viteză
mai mare și avem fenomenul contrar
și anume că raza reflectată se
întoarce în sens opus și Deci alfa-1
devine mai mic decât alpha2 putem
să ne închipuim că avem o serie
de alți astfel de suprafețe de
separare Deci ca avem o altă suprafață
aici care face tranziția la un
mediu cu viteza vetrei și așa mai
departe Deci obține încă Dacă vei
Unul este mai mare decât z 2 mai
mare decât V3 și așa mai departe
unghiurile scad și ele Alpha 1
mai mare decât Alpha 2 mai mare
decât Alpha 3 și așa mai departe
și invers Dacă vei Unul este mai
mic decât V2 mai mic decât vetrei
și așa mai departe unghiurile cresc
Alpha 1 mai mic decât Alpha 2 mai
mic decât Alpha 3 și așa mai departe
putem scrie în consecință că că
unghiul față de normală este direct
proporțional cu viteza de propagare
a luminii din acel mediu asta înseamnă
că dacă viteza scade unghiul scade
Dacă viteza crește unghiul crește
și în general Alfa împărțit la
z este aproximativ egal cu o constantă
în general se demonstrează și deocamdată
nu avem uneltele matematice pentru
a face acest lucru că relația exakta
este următoarea sinus de Alfa împărțit
la z este exact egal cu o constantă
și aceasta este prima forma a legii
cele de a doua refracție adică
Asta înseamnă mod direct că sinus
de Alfa 1 împărțit la 1 este egal
cu sinus de Alfa 2 împărțit la
v-2 sau în termenii din lecție
sinus de împărțit la v-1 este egal
cu sinus de aer 2 împărțit la V2
pentru a reduce cea de a doua formă
a celei de a doua lege refracție
în care viteza este înlocuită cu
indicii de refracție nu trebuie
decât să facem o simplă înlocuire
Deci ne scriem am arătat intuitiv
că ar trebui să fie adevărat că
sinus de i sau cynus de alfa-1
supra 1 este egal cu sinus de Alfa
2 sau notația din din lecție sinus
de r2 unghiul de refracție împărțit
la V2 aceasta este calitatea care
trebuie să fie corectăm ne reamintim
că indicii de refracție este definit
ca raportul dintre v și ce viteza
luminii made respectiv și viteza
luminii în vid și pentru a obține
aceasta înmulțim cu ce în ambele
părți a lega lui semnul egal ținem
că c sinus de împărțit la v-1 este
egal cu c sinus de aer 2 împărțit
la v-2 adică ce supravie sinus
de e este egal cu c supra V2 sinus
de aer 2 ceea ce înseamnă că n1
sinus de e este egal cu N2 sinus
de r2