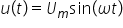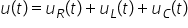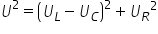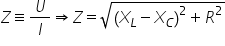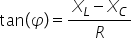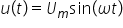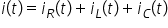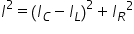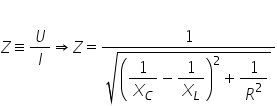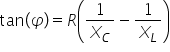Circuitele RLC serie şi paralel: impedanţa, diagrama fazorială.

În ciuda opta lecție de curent

alternativ am discutat despre circuitele

rlc serie și paralel circuitul

rlc serie este format bineînțeles

din din un rezistor o bobină și

un condensator conectat în așa

fel încât au aceeași intensitatea

curentului și conectată la o sursă

de curent alternativ cu tensiunea

valoarea momentană tensiunii curentului

alternativ va fi o funcție side

ala Omega fiind pulsația curentul

alternativ relația de bază a unui

circuit serie este aceea Că tensiunea

totală este egală cu suma tensiunilor

pe fiecare din cele trei elemente

Aceasta este o relație ce Folosește

modelul funcțiilor sinusoidale

pentru curentul alternativ putem

folosi celălalt model pe care îl

am introdus cel al florilor în

care fiecare mărime este reprezentată

pentru un fazor Care este un factor

ce se rotește întâlnit adică această

relație si din nou folosește funcții

sinusoidale poate fi scrisă în

formă aceasta unde fiecare mărime

este un Vector adică un fulger

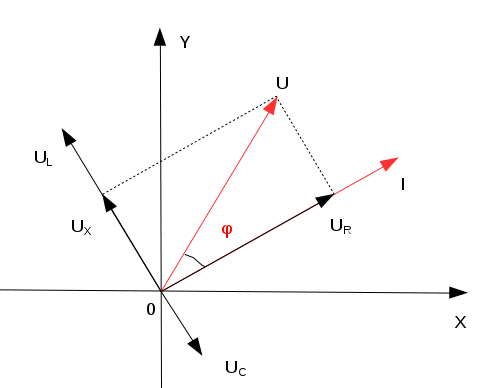
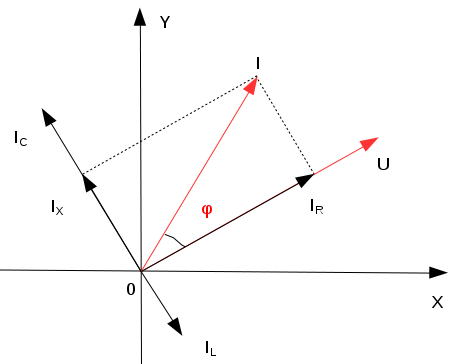
și să începem să Reprezentăm acești

fază Deci aceasta este diagrama

fazorială începem prin a reprezenta

fazorul intensității curentului

pentru că el este comun tuturor

din circuit după cum am văzut în

lecția trecută rezistența sau rezistorul

are o tensiune Ce este în fază

cu intensitatea curentului Deci

R fazorul tensiunii pe rezistor

sau în rezistor va fi coliniar

cu fazorul intensități faza zorii

celorlalte două elemente bobina

și condensatorul vor fi perpendicular

pe e pentru că am văzut Toată lecția

trecută că ei sunt defazati cu

pi pe 2 radiani adică 90 de grade

față de intensitatea curentului

din circuit unul de fazat în față

mai exact bobina este defazată

în față Iar condensatorul este

defazat în spate folosim aceste

informații pentru a începe Să calculăm

valoarea lui un pas dorului mai

exact deoarece u l și ucis în coliniari

introducem un nou fazor cu X definit

ca diferența dintre cei doi deci

asista este o x care este minus

si care bineînțeles la rândul lui

va fi perpendicular pe el și pe

muieri și e sunt coliniare în continuare

va fi suma vectorială dintre o

x și o y A deci este fazorul Care

este suma vectorială între which

și Where și datorită faptului că

avem un unghi de 90 de grade în

acest triunghi putem scrie unui

relația si de magnitudine lui Deci

pătrat este egal cu x pătrat plus

pătrat weeks Indiferența Deci o

pătrat va fi will pe 3 minus si

pătrat plus u r pătrat definim

scuze și mărime care se numește

impedanță raportul dintre tensiunea

totală și intensitatea totală din

tun circuit alternativ din această

ecuație folosind această definiție

obținem valoarea lui z a impedanței

în circuitul serie și anume radicali

din R pătrat plus pixel pătrat

music c pătrat unde pur și simplu

am folosit pe lângă Definiția lui

Zet definițiile reactanților XL

și XC XL și XC sunt tensiunile

pe el respectiv c împărțit la e

și legea lui om care spune că el

este egal cu u r împărțit la folosim

faptul că intensitatea curentului

este aceeași cu o putem simplifica

și obținem această relație această

relație bineînțeles ne dă numai

magnitudinea fazorul lui cu Următorul

pas este să stabilim orientarea

lui adică defazajul fi între tensiune

și intensitatea curentului folosim

același triunghi în care observăm

că tangent tangentă de c este egal

cu x împărțit la cu r Deci tangent

deși este o x această catetă în

pățit Laur ceea ce înseamnă înlocuind

valorile pentru x că tangent de

fi este XL minus x c împărțit la

aer este important De notat că

acest unghi ia orice valori între

minus și plus Pai asta înseamnă

că în funcție de valorile reactanților

din bobină și în condensator de

faza jul poate fi pozitiv adică

tensiunea totală poate fii în fața

intensității sau negativ adică

tensiunea totală poate fi în spatele

intensității totale din circuit

cauzele cazurile particulare ale

circuitelor LC serie RCS serie

și rl serie Deci combinații de

numai două din aceste trei elemente

se obțin foarte ușor punând ha

egal cu 0 rezistența respectiv

reactanți el a elementului pe care

vrem să scoatem din circuit exemplu

dacă vrem să obținem formulele

pentru un circuit RC serie punem

XL reactanța bobinei egală cu 0

în aceste formule să trecem la

circuitul rlc paralel este formată

din rezistență o bobină și un condensator

cuplate în paralel asta înseamnă

că ele au aceeași tensiune la borne

ceea ce diferă de data asta este

cazul opus celui circuitului rlc

serie ceea ce diferă este intensitatea

curentului prin fiecare din acest

acest aliment Deci avem că tensiunea

totală de la bornele întregului

circuit va avea aceeași formă uem

sinus de omega-3 dar ecuația de

la care plecăm este că intensitatea

totală din circuit este egală cu

suma intensităților pe fiecare

din cele trei elemente aceasta

este legea prima lege circov pentru

acest note intensitatea curentului

care intră în ore de gală cu suma

intensităților curenților care

ies din și la fel această ecuație

sta cu ecuația mărimilor momentane

exprimată în funcții sinusoidale

modelul funcțiilor sinusoidale

a curentul alternativ putem folosi

reprezentarea fazorială Deci această

ecuație în modelul fazorial se

scrie Salut următor Deci egal cu

a plus L plus c supra vectorială

toți vectori și Reprezentăm această

relație vectorială În diagrama

fazorială Deci aceasta este diagrama

fazorială de data aceasta începem

cu fazorul pentru tensiunea totală

pentru că el este comun întregului

circuit Deci toate cele trei elemente

au aceeași tensiune un Care este

tensiunea totală și Reprezentăm

cei trei cei trei fazori pentru

elementele r l și c iar își din

lecția trecută schimb de faza cele

pe care fiecare din cele trei intensitățile

au față de om Deci e r va fi coliniar

cu pentru că întru rezistor nu

există defazaj între tensiune și

intensitate a curentului iar aici

și el vor fi perpendicular pe u

Honda faza gegar cu piper 2 radiani

sau 90 de grade unul în față celălalt

în spate și procedăm la fel pentru

a calcula suma vectorială a celor

trei vectori și pentru a obține

fazorul intensității totale Deci

din nou introducem ex1 cantitate

1 mărime egală cu diferența dintre

a c și el Deci aceasta este x prințeselor

va fi dea lungul celor doi fazori

și va fi perpendicular pe el care

este coliniar cu intensitatea curentului

total va fi suma dintre x și Deci

facem suma vectorială e fiind suma

dintre x și modulul lui e pătrat

din acest triunghi în care putem

aplica teorema Pitagora Deci e

pătrat va fi x pătrat plus iar

pătrat adică e c minus a la pătrat

plus e r pătrat Folosind definiția

pentru impedanța Zet care din nou

prin definiție este raportul dintre

tensiunea totală și intensitatea

totală în tu în circuit alternativ

și înlocuind în această formulă

legile om pentru fiecare element

Deci ai va fi egal cu cu pătrat

pe z pătrat care va fi egal cu

Ice Care este împărțit la x si

y minus el Care este împărțit la

x la pătrat plus pătrat care este

cu pătrat împărțit la R pătrat

obținem după simplificarea tensiunii

Care este aceeași în tot circuitul

obținem această formulă pentru

impedanța unui circuit paralel

bineînțeles Na mai rămas o dată

ce am stabilit magnitudinea sau

lungimea pasului e trebuie să stabilim

orientarea lui în raport cu fazorul

tensiune Deci să calculăm fii folosim

același fel și anume că tangent

de fi tangentă de fii este egală

cu i x împărțit la iar și facem

același tip de înlocuiri și obținem

că tangentă de știi este egală

cu mulți cu 1 pe x c minus 1 pe

x aceleași comentarii două aceeași

două comentarii care am făcut pentru

circuitul rlc serie sunt valabile

și anume că acest unghi fii iaurt

ce valoare între minus și plus

fieri cămin între minus 180 și

plus 180 grade e în funcție de

valorile particulare ale lui x

c și cel Deci dacă e c este mai

mare decât el fii va fi pozitiv

și Deci intensitatea curentului

va fi defazată în față Față de

tensiune dacă el este mai mare

decât Ice atunci acest fi va fi

negativ și curentul va fi defazat

în spate față de tensiune Deci

va fi undeva în partea cealaltă