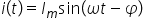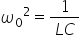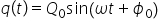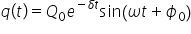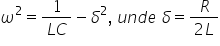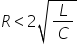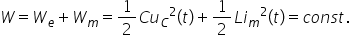Circuitul oscilant RLC. Oscilaţii electromagnetice.

în prima lecție despre oscilații

și unde electromagnetice vom discuta

discuta despre circuitul oscilant

și despre oscilații electromagnetice

în circuitele de curent alternativ

sensul în care electroni parcurge

circuitul se schimbă periodic cu

pulsația Omega generând astfel

un curent oscilant acest cuvânt

aceste cuvinte curent ocland arată

faptul că electronii au mișcare

periodică oscilatorie prin circuitul

nostru aceasta se vede și Din formula

intensității curentului în intensitate

are o formă sinusoidală de timp

și dacă luăm în considerare definiția

intensității este prin definiție

variația sarcinii electrice în

unitatea de timp adică sarcina

electrică elementară cea cărată

de un electron înmulțită cu variația

numărului de electroni în unitatea

de timp asta înseamnă că dacă considerăm

un conductor sau orice element

alt circuitul nostru de curent

alternativ printro pentru secțiune

din acest conductor în circuitul

nostru electronii vor avea o mișcare

oscilatorie Deci vor parcurge în

felul acesta oscilator această

secțiune fixă din circuit iar intensitatea

curentului ne Arată că numărul

de electroni în unitatea de timp

este o funcție sinusoidal Deci

în mod în modul cel mai direct

electronii oscilează în circuitul

nostru de curent alternativ aceste

oscilație electromagnetice puți

observate direct cunoști la Sacoșu

scop ceea ce vedeți în această

imagine este un urșilor scop conectat

la un element de circuit alternativ

și vedem direct pe ecranul osciloscopului

forma intensității sau tensiunii

în curent alternativ Care este

forma periodică Ele pot fi de asemenea

studiate direct cu așa numitul

circuit oscilant care este prezentat

în această imagine circuitul oscilant

este format din un condensator

și o bobină o bobină reală are

și o rezistență R firele bobinei

înfășurările o bobinei în fond

depun o rezistență la trecerea

curentului prin ele și această

rezistență am reprezentat schematic

separat În diagrama noastră dar

în principal un circuit oscilant

are un condensator și o bobină

rezistența apărând din nou datorită

rezistenței efectiv a bobinei la

trecerea curentului avem de asemenea

o sursă de curent continuu și două

întrerupătoare notate cu ca unul

și cadă în faza inițială se închide

ca unul și se păstrează ca 2 deschis

asta înseamnă că sursa de curent

continuu i va încărca condensatorul

ce deci între Polul pozitiv și

Polul negativ al sursei se creează

un curent continuu care va încărca

condensatorul ce Deci obținem popularizare

a plăcilor armăturilor condensatorului

în faza a doua a experimentului

deschidem ca unu și închidem Ca

doi de ce în felul acesta păstrăm

numai partea din circuit Ce conține

bobina și condensatorul condensatorul

se descarcă atunci și se în care

încarcă cu sarcini de polaritate

inversă datorită auto inducție

din bobină de ce obținem oscilație

a curentului electric o ceva ție

de tip curent alternativ în acest

circuit LC felul cum are loc Sau

mecanisme prin care are loc această

oscilați electromagnetic are la

bază după cum am spus auto inducția

din Baban Deci mai exact în mâncare

se închide ca 2 condensatorul se

va descărca stabilind un curent

e acest curent e va produce este

un curent de inducție și va produce

un câmp magnetic pe axa bobinei

după cum am discutat în lecțiile

de despre curent alternativ și

fenomenul de inducție electromagnetică

Dar acest câmp magnetic indus Care

este variabil la rândul său de

ce acest curent este dependent

de timp va produce de asemeni un

curent electric indus Care este

dependent de timp deci după ce

condensatorul ce se descarcă apare

în circuitul oscilant un alt curent

datorat curentului electric indus

de sens opus Deci curentul in dus

va avea sens opus și va încărca

armăturile condensatorului cu polarității

invers deci pe minus și plus în

loc de plus și minus după ce acțiunea

acestui curent indus dispare bineînțeles

vom avea iarăși o descărcare A

condensatorului dar curentul de

descărcare a condensatorului va

fi invers bineînțeles pentru că

polarități lac unde de la de pe

armăturile condensatorului sunt

invers sunt opuse si felul acesta

avem o și la ție Ce are la bază

fenomenul de auto inducție din

bobină oscilație a curentului în

acest circuit dacă rezistența bobinei

este 0 atunci circuitul oscilant

LC este ideal aceste acest curent

dependenți de timbre 5 curenți

alternativi sunt egali și atunci

oscilațiile electromagnetice se

numesc libere și după cum am văzut

El e o pulsație egală cu 1 supra

radical din LC dacă în schimb bobina

are o rezistență CC în realitate

întotdeauna se întâmplă atunci

circuitul oscilant se numește real

și curenții uși curentul din circuitul

oscilant scade în timp datorită

efectului Joule energia înmagazinată

în sistem se pierde în timp datorită

efectului Joule încălzirea bobinei

și atunci avem de a face cu oscilații

electromagnetice amortizat Haideți

să discutăm un pic despre ele Deci

intru în circuit oscilant real

ecuația tensiunilor este următoarea

intensitatea este aceeași prin

toate elementele r l și c pensiunile

să se adună și obținem 0 pentru

că nu avem o sursă în acest circuit

Deci tensiunea pe bobină plus căderea

de tensiune pe rezistor Care este

de fapt în realitate tot în bobină

Deci când vorbim de hernie FM are

rezistența electrică a firelor

din bobină plus tensiunea pe condensator

sunt 0 dacă film explicit obținem

următoarea ecuație el de la de

ten din bobină plus r e parcă de

tensiune rezistor sau pe rezistența

bobinei plus fiu împărțit la c

Care este tensiunea de pe condensator

este egal cu 0 folosind Dino definiția

intensității De ce este prin definiție

de q ladite obținem următoarea

ecuație derivată de ordinul doi

a sarcinii electrice din circuitul

oscilant plus R derivată de ordin

1 a sarcinii raportată la timp

plus sarcină în sine Care este

o funcție de timp împărțită la

capacitatea condensatorului este

egal cu zero aceasta este ecuație

diferențială de ordinul doi a sarcinii

electrice care se rezolvă și obținem

următoarea soluție fiu ca funcție

de timp sarcină electrică este

o funcție sinusoidală cu anumită

pulsația Omega 0 înmulțită cu o

amplitudine Care este dependentă

de timp și anume q0 Care este sarcina

maximă la momentul t egal cu 0

mulți tool cu o funcție exponențial

descrescătoare de timp în care

cei doi parametri care descriu

această funcție sunt Omega 0 și

Delta fi 0 este faza inițială Deci

Omega 0 din rezolvarea acestei

ecuații rezultă că este egal cu

1 supra l c minus un factor de

corecție acest Delta numit coeficient

de atenuare Deci pulsația oscilațiilor

amortizate este egală cu pulsația

oscilațiilor libere scăzută cu

un anumit Factor de corecție Delta

care se numește coeficient de atenuare

și este egal cu raportul dintre

rezistența era bobinei și de două

ori impedanța a se observă că dacă

punem condiția ca Omega 0 să fie

mai mare mai mare ca 0 atunci obținem

următoarea condiție aer trebuie

să fac să fie mai mic decât doi

radical din lpc Deci efectiv Omega

0 voi scrie aici Omega 0 la pătrat

mai mare ca 0 unde prima megazar.ro

înțeleg acest omegarom inchide

să trag o săgeată Așa Deci acest

Omega Zorro mai mare decât 0 implică

că 1 supra l c minus iar pătrat

împărțit la 4 L pătrat trebuie

să fie mai mare decât 0 de unde

rezultă această condiții Ce se

întâmplă dacă totuși ele este mai

mare decât această valoare atunci

avem o amortizare foarte rapidă

a curentului și numai obținem nicio

oscilații deci pur și simplu curentul

sau sarcină electrică cade direct

către 0 după o funcție exponențială

foarte rapid Deci dacă reprezentând

grafic această soluție obținem

următoarea dependență temporală

Deci ce vedeți cu verde este q

de te ca funcție de ten și este

între adevărul o funcție sinusoidală

a cărei perioadă este dată de această

pulsație Deci perioada funcții

oscilațiilor magnetice amortizat

este mai mare decât a celor libere

pentru că pulsație este mai mic

Vă aduc aminte că Omega este egal

cu doi pipetei Deci o pulsație

mai mică înseamnă o perioadă mai

mare obținem Deci o funcție sinusoidală

dar cu o perioadă ceva mai mare

mai important totuși a cărei amplitudine

scadent aici numele de amortizate

scăderea amplitudinea oscilațiilor

în timp este dată de această funcție

exponențială descrisă de coeficientul

de atenuare de alta și reprezentată

grafic prin această linie roșie

întreruptă din nou ciudate funcția

sarcinii de timp arată acesta prezentat

cu culoare verde În graficul acesta

în cazul în care el îndeplinește

această rezistența îndeplinește

această condiție dacă nu îndeplinește

atunci pur și simplu obținem graficul

de culoare verde va fi o funcție

exponențială foarte rapid descrescătoare

și de curentul va scădea bruscă

trezea dacă înlocuim sursa de curent

continuu din grafic din diagrama

anterioară cu o sursă de curent

alternativ a cărei tensiune este

o funcție sinusoidală de Omega

te astfel încât pulsație e Omega

să fie egal cu Omega 0 acest Omega

0 atunci obținem o Sila ții electromagnetice

forțate asta înseamnă că la momentul

oportun furnizăm sistemului Care

este între oscilații electromagnetică

amortizată suficientă energie pentru

a compensa aceste pierderi din

sistem și obțin o dependență constantă

de timp amplitudinii deci obținem

o dependență de timp tipică oscilațiilor

electromagnetice libere cu amplitudine

constantă totuși bineînțeles rezistența

în cazul acesta este diferența

de 0 licitațiile ar fi amortizate

pierdem energie totuși ele nu sunt

amortizate pentru că energia Care

este pierdută este furnizată de

către sursa noastră de curent alternativ

acesta este modul tipic de funcționare

a unui sistem de curent alternativ

avem rezistențe dar avem și surse

care compensează pierdere provocate

de aceste rezistenți Haideți să

discutăm despre interpretarea energetică

a oscilațiilor libere deci vorbim

despre oscilații libere în care

rezistența din sistem este neglijat

energia magnetică este prin definiție

după cum am discutat în lecțiile

de curent alternativ egală cu 1

pe 2 L ori e la pătrat închizând

intensitatea curentului prin bobina

la între respectiv care poate fi

scrisă bineînțeles în acest fel

am scris explicit intensitatea

curentului Care este o funcție

sinusoida energia electrică este

înmagazinată în circuit oscilant

pe condensator și va fi egală din

nou după cum am discutat în accident

alternativ cu 1 pe 2 capacitatea

condensatorului înmulțită cu tensiunea

la pătrat pe condensator scriind

efectiv ecuația sau forma pentru

tensiunea pe condensator obține

următoarea formulă din care observăm

că am obținut o un defazaj de minus

fie pe doi sau minus 90 de grade

aceasta datorită faptului că tensiunea

și intensitatea un condensator

aflat în curent alternativ sunt

defazate cubi pe 2 mai exact tensiunea

este defazată în spatele intensității

cu pi pe 2 intensitatea de pe bobină

și intensitatea de pe condensator

sunt egale pentru un circuit oscilant

și atunci putem scrie această ecuație

folosind în continuare faptul că

sinus de Alfa minus pi pe 2 este

egal cu cosinus de Alfa Aceasta

este o identitate trigonometrică

putem Scrie forma finală a energiei

electrice în circuit oscilant deocamdată

nu am folosit faptul că oscilațiile

sunt liber le vom folosi imediat

pentru a demonstra că amplitudinea

energiei magnetice este egală cu

amplitudinea energiei electrice

în cazul oscilațiilor libere vă

reamintesc în acest caz Omega 0

este egal cu 1 pe radical din LC

Deci scriem ce înmulțit cu reactanța

capacitivă la Pătrat ca fiind egal

cu c ori 1 supra Omega la pătrat

pătrat aceasta este pur și simplu

definiția reactanța capacitivă

1 pe Omega C dar în cazul și lați

lor libere pulsația are această

valoare și deci putem scrie mai

departe ca unul pe c l c care este

egal cu el deci în cazul rezultă

că în cazul oscilațiilor libere

în care pulsații are această valoare

amplitudinile energiei magnetice

și energiei electrice sunt egale

și egal cu 1 pe 2 l i m la pătrat

Deci aceasta este egal cu w e 0

Deci amplitudinile lor sunt egale

în concluzie energia electromagnetică

a circuitului oscilant aflat întru

oscilație liberă care prin definiție

suma dintre cele două energii va

fi egală cu această valoare maximă

înmulțită cu sinus la pătrat plus

aceeași valoare maxim munții cu

Constanța pătrat dar după cum știm

sinus pătrat plus cosinus pătrat

de Orice unghi este egal cu unu

Deci obține încă energie electromagnetică

este această valoare maximă care

ești o constantă nu depinde de

timp în consecință dacă Reprezentăm

grafic cu verde valoarea momentană

a energiei magnetice Deci această

funcție obținem o variație sinusoidală

mai exact un ce nu pot Dar semn

dacă Reprezentăm cu albastru valoarea

momentană a energiei electrice

din sistem obținem această dependență

Deci funcția este aceea aceasta

iar suma lor este reprezentantul

cu roșu reprezentată cu roșu și

este energia totală electromagnetică

Care este o constantă În consecință

energia oscilațiilor electromagnetice

libere ale circuitului oscilant

LC ideal Artur nează după cum se

vede între forma magnetică în bobină

și cea electrică de pe condensator

dar având o sumă constant i se

vede acum Pe măsură ce Spre exemplu

energia magnetică scade ce ai electrică

crește cu aceeași valoare astfel

încât suma lor să fie constantă

Deci avem efectiv o un transfer

alternative oscilant de energie

între bobină și condensator